题目内容
已知定义在R上的函数y＝f(x)满足以下三个条件：①对于任意的x∈R，都有f(x＋1)＝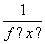
；②函数y＝f(x＋1)的图象关于y轴对称；③对于任意的x1，x2∈[0,1]，且x1<x2，都有f(x1)>f(x2)，则f
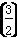，f(2)，f(3)从小到大的关系是________．
f(3)<f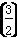<f(2)
[解析] 由①得f(x＋2)＝f(x＋1＋1)＝
＝f(x)，所以函数f(x)的周期为2.
因为函数y＝f(x＋1)的图象关于y轴对称，将函数y＝f(x＋1)的图象向右平移一个单位即得y＝f(x)的图象，所以函数y＝f(x)的图象关于x＝1对称；根据③可知函数f(x)在[0,1]上为减函数，又结合②知，函数f(x)在[1,2]上为增函数．
因为f(3)＝f(2＋1)＝f(1)，在区间[1,2]上，1<
<2，
所以f(1)<f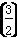<f(2)，
即f(3)<f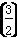<f(2)．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
相关题目
n展开式的二项式系数之和为32，常数项为80，则a的值为( )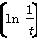
≤2f(1)，那么t的取值范围是________．
ln(1－x)的定义域是( )
的图象可能是( )
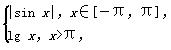
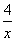是定义在集合M＝
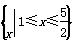上的两个函数．对任意的x∈M，存在常数x0∈M，使得f(x)≥f(x0)，g(x)≥g(x0)，且f(x0)＝g(x0)．则函数f(x)在集合M上的最大值为( )
B．4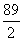 
的前n项和为Sn，若S2n＋1－Sn≤
对n∈N*恒成立，则正整数m的最小值是________．