题目内容
设两非零向量
和
不共线,如果
=
+
,
=3(
-
),
=2
+8
,求证:A、B、D三点共线.
| a |
| b |
| AB |
| a |
| b |
| CD |
| a |
| b |
| BC |
| a |
| b |
分析:利用向量的加法运算结合已知条件求出向量
,
,得到
=
,由共线向量基本定理得到
与
共线,从而证明A、B、D三点共线.
| AD |
| BD |
| AD |
| 6 |
| 5 |
| BD |
| AD |
| BD |
解答:证明:∵
=
+
,
=3(
-
),
=2
+8
,
∴
=
+
=(
+
)+(2
+8
)=3
+9
=3(
+3
),
=
+
=3(
+3
)+3(
-
)=6(
+
).
=
+
=(2
+8
)+3(
-
)=5(
+
).
∵
=
•5(
+
)=
,
∴
与
共线,即A、B、D三点共线.
| AB |
| a |
| b |
| CD |
| a |
| b |
| BC |
| a |
| b |
∴
| AC |
| AB |
| BC |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| AD |
| AC |
| CD |
| a |
| b |
| a |
| b |
| a |
| b |
| BD |
| BC |
| CD |
| a |
| b |
| a |
| b |
| a |
| b |
∵
| AD |
| 6 |
| 5 |
| a |
| b |
| 6 |
| 5 |
| BD |
∴
| AD |
| BD |
点评:本题考查了平行向量与共线向量,考查了共线向量基本定理,是基础的证明题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
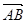 =
= +
+  ,
,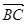 =2
=2 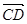 =3(
=3(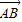 =e1+e2,
=e1+e2,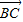 =2e1+8e2,
=2e1+8e2,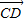 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;