题目内容
已知函数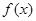 是定义在R上的函数,其最小正周期为3,且
是定义在R上的函数,其最小正周期为3,且 时,
时,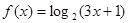 ,则f(2014)=( )
,则f(2014)=( )
| A.4 | B.2 | C.-2 | D.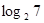 |
B.
解析试题分析:因为函数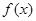 是定义在R上的函数,其最小正周期为3.所以f(x)=f(x+3).所以f(2014)=f(1).又因为且
是定义在R上的函数,其最小正周期为3.所以f(x)=f(x+3).所以f(2014)=f(1).又因为且 时,
时,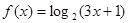 ,所以f(1)=
,所以f(1)= .即选B.
.即选B.
考点:1.周期函数.2.分段函数的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 ,则
,则 等于( )
等于( )
| A.1 | B.-1 | C.2 | D.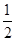 |
已知函数
 数列
数列 满足
满足 ,且
,且 是单调递增数列,则实数
是单调递增数列,则实数 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
已知偶函数 在区间
在区间 单调增加,则满足
单调增加,则满足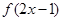 <
<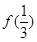 的
的 取值范围是( )
取值范围是( )
A.(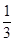 , ,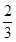 ) ) | B.[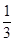 , ,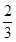 ) ) | C.(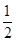 , ,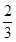 ) ) | D.[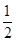 , ,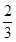 ) ) |
已知函数 是偶函数,当
是偶函数,当 时,函数
时,函数 单调递减,设
单调递减,设 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
| A.c<a<b | B.a<b<c | C.a<c<b | D.c<b<a |
如图是函数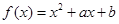 的部分图像,函数
的部分图像,函数 的零点所在的区间是
的零点所在的区间是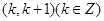 ,则
,则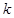 的值为( )
的值为( )
A. 1或0 1或0 | B.0 | C. 1或1 1或1 | D.0或1 |
若函数 (
( )是奇函数,函数
)是奇函数,函数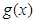 (
( )是偶函数,则( )
)是偶函数,则( )
A.函数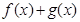 是奇函数 是奇函数 | B.函数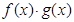 是奇函数 是奇函数 |
C.函数 是奇函数 是奇函数 | D.函数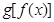 是奇函数 是奇函数 |
为了得到函数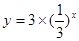 的图象,可以把函数
的图象,可以把函数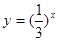 的图象( )
的图象( )
| A.向左平移3个单位长度 | B.向右平移3个单位长度 |
| C.向左平移1个单位长度 | D.向右平移1个单位长度 |
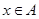 ,
,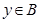 ,(
,(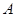 、
、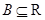 )有唯一确定的
)有唯一确定的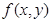 与之对应,称
与之对应,称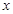 、
、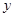 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数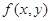 为关于实数
为关于实数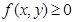 ,当且仅当
,当且仅当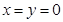 时取等号;
时取等号;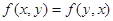 ;
;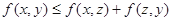 对任意的实数z均成立.
对任意的实数z均成立.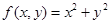 ;②
;②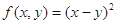 ;③
;③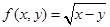 ;
; .能够成为关于的
.能够成为关于的