Question

已知曲线C₁：y=x²与C₂:y=-(x-2)²,若直线l与C₁、C₂都相切,求l的方程.

Answer 1

分析：本题主要考查导数几何意义的应用.要求具有某种性质的切线,只需求出对应的x₀即可,一般要求出x₀所需满足的方程或方程组,解之即可.

解：设直线l与C₁相切于点(x₁,x₁²),

∵y=x²,∴y′=2x.

∴=2x₁.    

∴l：y-x₁²=2x1(x-x₁),即y=2x₁x-x₁².     

设直线l与C₂相切于点(x₂,-(x₂-2)²),

∵y=-(x-2)²,

∴y′=-2(x-2).

∴=-2(x₂-2).                  

∴l：y+(x₂-2)²=-2(x₂-2)(x-x₂),

即y=-2(x₂-2)x+x₂²-4.                 

比较l的两个方程,应有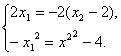

将x₁=2-x₂代入第二个方程,得-(2-x₂)²=x₂²-4,

解得x₂=0或x₂=2,于是x₁=2或x₁=0.   

当x₁=2,x₂=0时,直线l经过两点(2,4)、(0,-4),

∴直线l的方程为y=4x-4;

当x₁=0,x₂=2时,直线l经过(0,0)、(2,0)两点.

∴直线l的方程为y=0.