题目内容
已知曲线c1：y=ex，曲线c2：y=cosx，则由曲线c1，c2和直线x=
在第一象限所围成的封闭图形的面积为
| π |
| 2 |
e
-2
| π |
| 2 |
e
-2
．| π |
| 2 |
分析：作出图形，则所求的封闭图形的面积S=
(ex-cosx)dx，解出即可．
| ∫ |
0 |
解答：解：作出曲线c1：y=ex，曲线c2：y=cosx，则由曲线c1，c2和直线x=
，如图所示：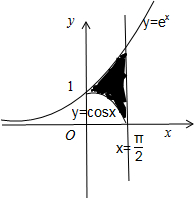
则所求的封闭图形的面积S=
(ex-cosx)dx=(ex-sinx)
=e
-2．
故答案为e
-2．
| π |
| 2 |
则所求的封闭图形的面积S=
| ∫ |
0 |
| | |
0 |
| π |
| 2 |
故答案为e
| π |
| 2 |
点评：理解定积分的意义是解题的关键．
练习册系列答案
相关题目
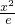+e（e为自然对数的底数），曲线C2：y=2elnx和直线m：y=2x．
+e（e为自然对数的底数），曲线C2：y=2elnx和直线m：y=2x．