题目内容
(满分13分)已知函数
(1)求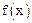 的单调区间;
的单调区间;
(2)记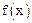 在区间
在区间
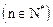 上的最小值为
上的最小值为 令
令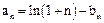 ;
;
①如果对一切n,不等式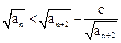 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
②求证: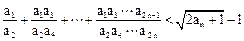 。
。

(1)求
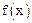 的单调区间;
的单调区间;(2)记
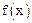 在区间
在区间
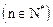 上的最小值为
上的最小值为 令
令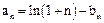 ;
;①如果对一切n,不等式
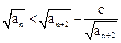 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;②求证:
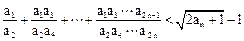 。
。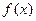 的单调递增区间为
的单调递增区间为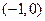 ,
,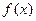 的单调递增区间为(0,+
的单调递增区间为(0,+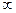 ),
),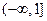
解:(I)因为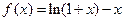 ,所以函数定义域为
,所以函数定义域为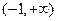 ,且
,且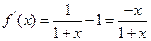 。
。
由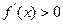 得
得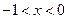 ,
,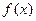 的单调递增区间为
的单调递增区间为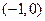 ;
;
由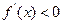 <0得
<0得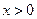 ,
,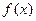 的单调递增区间为(0,+
的单调递增区间为(0,+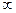 ).
).
(II) 因为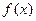 在
在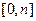 上是减函数,所以
上是减函数,所以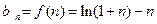
则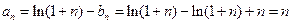 .
.
①: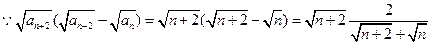
>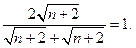
又lim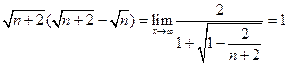 ,
,
因此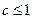 ,即实数c的取值范围是
,即实数c的取值范围是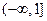 .
.
② : 由① 知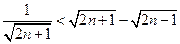 ③
③
因为[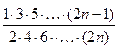 ]2
]2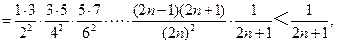
所以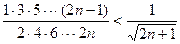 <
<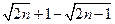 (n
(n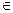 N*),
N*),
则 <
<
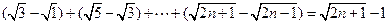
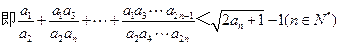

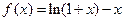 ,所以函数定义域为
,所以函数定义域为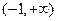 ,且
,且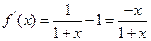 。
。由
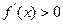 得
得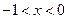 ,
,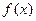 的单调递增区间为
的单调递增区间为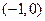 ;
;由
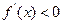 <0得
<0得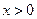 ,
,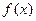 的单调递增区间为(0,+
的单调递增区间为(0,+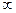 ).
).(II) 因为
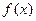 在
在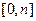 上是减函数,所以
上是减函数,所以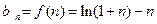
则
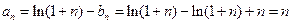 .
.①:
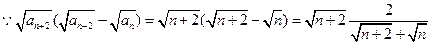
>
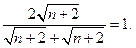
又lim
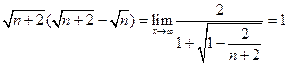 ,
,因此
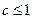 ,即实数c的取值范围是
,即实数c的取值范围是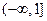 .
.② : 由① 知
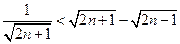 ③
③因为[
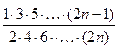 ]2
]2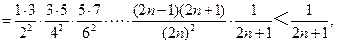
所以
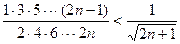 <
<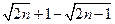 (n
(n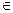 N*),
N*),则
 <
<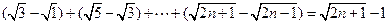
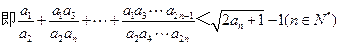


练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
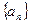 中,
中,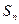 是其前
是其前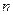 项和,且
项和,且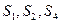 成等比数列.
成等比数列.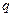 ;
;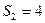 ,求等差数列
,求等差数列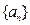 中,
中,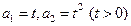 。
。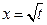 是函数
是函数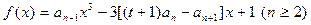 的一个极值点。
的一个极值点。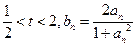 ,求证:对于任意正整数
,求证:对于任意正整数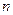 ,
,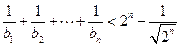 ;
;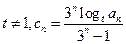 ,证明:
,证明: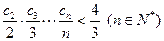
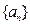 满足
满足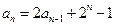
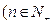 ,且
,且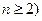 ,
,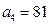 .
.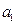 ,
,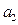 ,
, ;
;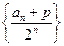 为等差数列,求实数
为等差数列,求实数 的值;
的值;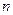 项和
项和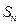
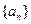 的前
的前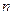 项和为
项和为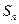 ,且
,且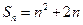 .数列
.数列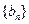 中,
中,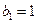 ,
,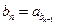
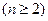 .(1)求数列
.(1)求数列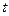 使数列
使数列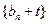 是等比数列,求数列
是等比数列,求数列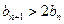 ;②
;②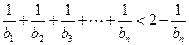 .
.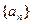 的前
的前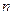 项和为
项和为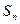 ,且
,且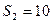 ,
,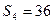 ,则过点
,则过点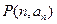 和
和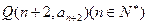 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )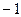 ,
,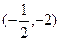

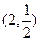
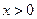 ,
,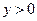 ,
,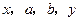 成等差数列,
成等差数列,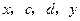 成等比数列,
成等比数列,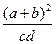 的最小值是( )
的最小值是( )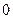
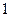
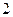

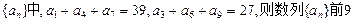 项的和
项的和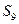 等于( )
等于( )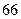
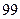
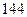
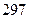
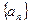 中,公差
中,公差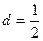 ,前
,前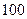 项的和
项的和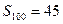 ,
,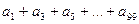 =_____________
=_____________