题目内容
13.过抛物线y2=4x焦点F的直线交抛物线于A、B两点,交其准线于点C,且A、C位于x轴同侧,若|AC|=2|AF|,则|BF|等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由题意可知:|AC|=2|AF|,则∠ACD=$\frac{π}{6}$,利用三角形相似关系可知丨AF丨=丨AD丨=$\frac{4}{3}$,直线AB的切斜角$\frac{π}{3}$,设直线l方程,代入椭圆方程,利用韦达定理及抛物线弦长公式求得丨AB丨,即可求得|BF|.
解答 解:抛物线y2=4x焦点F(1,0),准线方程l:x=-1,准线l与x轴交于H点,
过A和B做AD⊥l,BE⊥l,
由抛物线的定义可知:丨AF丨=丨AD丨,丨BF丨=丨BE丨,
|AC|=2|AF|,即|AC|=2|AD|,
则∠ACD=$\frac{π}{6}$,由丨HF丨=p=2,
∴$\frac{丨HF丨}{丨AD丨}$=$\frac{丨CF丨}{丨AC丨}$=$\frac{3}{2}$,
则丨AF丨=丨AD丨=$\frac{4}{3}$,
设直线AB的方程y=$\sqrt{3}$(x-1),
$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=\sqrt{3}(x-1)}\end{array}\right.$,整理得:3x2-10x+1=0,
则x1+x2=$\frac{10}{3}$,
由抛物线的性质可知:丨AB丨=x1+x2+p=$\frac{16}{3}$,
∴丨AF丨+丨BF丨=$\frac{16}{3}$,解得:丨BF丨=4,
故选C.
点评 本题考查抛物线的性质,直线与抛物线的位置关系,考查相似三角形的性质,考查计算能力,数形结合思想,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}1,x>0\\-1,x<0\end{array}\right.$,设$g(x)=\frac{f(x)}{x^2}$,则g(x)是( )
| A. | 奇函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| B. | 奇函数,在(-∞,0)上递减,在(0,+∞)上递减 | |
| C. | 偶函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| D. | 偶函数,在(-∞,0)上递减,在(0,+∞)上递减 |
2.已知l、m是两直线,α是平面,l∥α,m⊥α,则直线l、m的关系是( )
| A. | l∥m | B. | l⊥m | C. | l与m是相交直线 | D. | l与m是异面直线 |
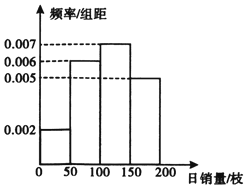 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.