题目内容
若曲线f(x)=xsinx+1在x=
处的切线与直线2x-ay+1=0互相垂直,则实数a等于( )
| π |
| 2 |
| A、-2 | B、-1 | C、1 | D、2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:欲求出实数a,只须求出其斜率即可,故先利用导数求出在切点处的导函数值,再结合导数的几何意义以及两直线垂直斜率之积为-1,即可求出切线的斜率.从而问题解决.
解答:
解:f′(x)=sinx+xcosx,
∵曲线在x=
处的切线与直线2x-ay+1=0互相垂直,
∴根据导数几何意义得:f′(
)=-
,即:1=-
,
解得:a=-2.
故选A.
∵曲线在x=
| π |
| 2 |
∴根据导数几何意义得:f′(
| π |
| 2 |
| a |
| 2 |
| a |
| 2 |
解得:a=-2.
故选A.
点评:本题主要考查垂直直线的斜率关系、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知复数Z=1-i,则
=( )
| Z2-2Z |
| Z-1 |
| A、2 | B、-2 | C、-2i | D、2i |
函数f(x)=log2x在区间[1,2]上的最小值是( )
| A、-1 | B、0 | C、1 | D、2 |
在△ABC中,已知a=6,b=8,A=30°,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f(x)=ex(sinx-cosx)(0≤x≤40π),则函数f(x)各极小值点之和为( )
| A、380π | B、800π |
| C、420π | D、820π |
已知sin(θ+π)<0,cos(θ-π)>0,则θ是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
“猿用肺呼吸,猫用肺呼吸,象用肺呼吸,所以一切哺乳动物都用肺呼吸”.此推理方法是( )
| A、完全归纳推理 | B、归纳推理 |
| C、类比推理 | D、演绎推理 |
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )
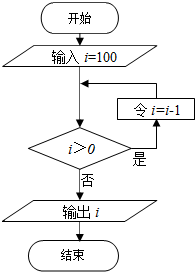

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |