题目内容
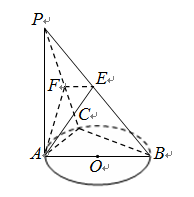
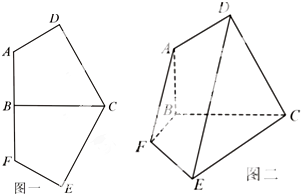
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=
,将此图形沿BC折叠成直二面角,连接AF、DE得到几何体(如图2).
(1)证明:AF∥平面DEC;
(2)求二面角E-AD-B的余弦值.
| 3 |
(1)证明:AF∥平面DEC;
(2)求二面角E-AD-B的余弦值.

(1)证明:以B为坐标原点,分别以BF,BC,BA为x轴、y轴、z轴的正方向,
建立如图所示的空间直角坐标系,
由已知条件与平面向何知识得:
A(0,0,1),F(1,0,0),D(0,
,
),E(
,
,0),
∴
=(1,0,-1),
=(
,0,-
),
∴
=
,∴AF∥DE,
又DE?平面DCE,且AF不包含平面DCE,
∴AF∥平面DEC.
(2)由(Ⅰ)得A、D、E、F四点共面,
=(1,0,-1),
=(0,
,
),
设平面ADEF的法向量
=(x,y,z),
则
,
令y=-1,得
=(
,-1,
),
由已知得平面ABCD的一个法向量为
=(1,0,0),
∴cos<
,
>=
=
,
∴二面角E-AD-B的余弦值为
.
建立如图所示的空间直角坐标系,

由已知条件与平面向何知识得:
A(0,0,1),F(1,0,0),D(0,
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
∴
| AF |
| DE |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| AF |
| 2 |
| 3 |
| DE |
又DE?平面DCE,且AF不包含平面DCE,
∴AF∥平面DEC.
(2)由(Ⅰ)得A、D、E、F四点共面,
| AF |
| AD |
| ||
| 2 |
| 1 |
| 2 |
设平面ADEF的法向量
| n |
则
|
令y=-1,得
| n |
| 3 |
| 3 |
由已知得平面ABCD的一个法向量为
| m |
∴cos<
| n |
| m |
| ||
|
| ||
| 7 |
∴二面角E-AD-B的余弦值为
| ||
| 7 |

练习册系列答案
相关题目


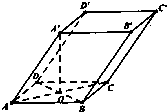
 且
且 ,给出下列命题:
,给出下列命题: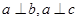 则
则 ②
②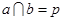 则
则
 ④若
④若 则
则