题目内容
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是________.


60°
连接AB1,易知AB1∥EF,

连接B1C交BC1于点G,取AC的中点H,连接GH,则GH∥AB1∥EF.故∠HGB(或其补角)即为EF和BG所成角.设AB=BC=AA1=a,连接HB,在△GHB中,易知GH=HB=BG= a,
a,
故两直线所成的角即为∠HGB=60°.

连接B1C交BC1于点G,取AC的中点H,连接GH,则GH∥AB1∥EF.故∠HGB(或其补角)即为EF和BG所成角.设AB=BC=AA1=a,连接HB,在△GHB中,易知GH=HB=BG=
 a,
a,故两直线所成的角即为∠HGB=60°.

练习册系列答案
相关题目
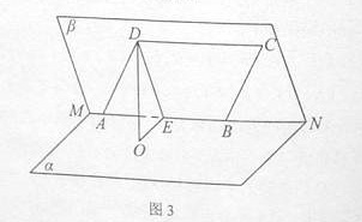
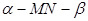 的大小为
的大小为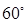 ,菱形
,菱形 在面
在面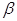 内,
内,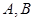 两点在棱
两点在棱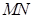 上,
上,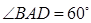 ,
,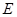 是
是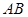 的中点,
的中点,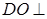 面
面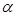 ,垂足为
,垂足为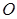 .
.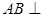 平面
平面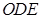 ;
;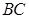 与
与 所成角的余弦值.
所成角的余弦值.