题目内容
椭圆 的离心率为
的离心率为 ,长轴长为12,直线y=kx-4与椭圆交于A,B,弦AB的长为
,长轴长为12,直线y=kx-4与椭圆交于A,B,弦AB的长为 ,求此直线的斜率.
,求此直线的斜率.
解:由长轴长为12,得a=6,由离心率为 ,得
,得 ,解得c=
,解得c= ,所以b2=a2-c2=36-27=9,
,所以b2=a2-c2=36-27=9,
所以椭圆方程为: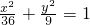 ,
,
设A(x1,y1),B(x1,y1),由 ,消掉y得(1+4k2)x2-32kx+28=0,则
,消掉y得(1+4k2)x2-32kx+28=0,则 ,
, ,
,
△=(32k)2-4×28(1+4k2)=16(36k2-7),
|AB|= =
= •
•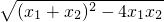 =
= •
• =
= .
.
解得k= ,经验证△>0成立,
,经验证△>0成立,
故直线斜率为: .
.
分析:根据长轴长及离心率可求出椭圆方程,根据弦长公式可用k表示出弦长,令其为 ,解出即可,注意检验.
,解出即可,注意检验.
点评:本题考查椭圆方程的求解及直线与圆锥曲线的位置关系,考查弦长公式,考查学生的运算能力,本题属中档题.
 ,得
,得 ,解得c=
,解得c= ,所以b2=a2-c2=36-27=9,
,所以b2=a2-c2=36-27=9,所以椭圆方程为:
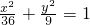 ,
,设A(x1,y1),B(x1,y1),由
 ,消掉y得(1+4k2)x2-32kx+28=0,则
,消掉y得(1+4k2)x2-32kx+28=0,则 ,
, ,
,△=(32k)2-4×28(1+4k2)=16(36k2-7),
|AB|=
 =
= •
•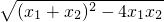 =
= •
• =
= .
.解得k=
 ,经验证△>0成立,
,经验证△>0成立,故直线斜率为:
 .
.分析:根据长轴长及离心率可求出椭圆方程,根据弦长公式可用k表示出弦长,令其为
 ,解出即可,注意检验.
,解出即可,注意检验.点评:本题考查椭圆方程的求解及直线与圆锥曲线的位置关系,考查弦长公式,考查学生的运算能力,本题属中档题.

练习册系列答案
相关题目
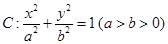 的离心率为
的离心率为 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为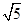 .
. 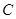 的方程;
的方程; 的直线
的直线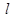 与椭圆
与椭圆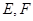 ,
,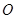 为坐标原点,若
为坐标原点,若 为直角三角形,求直线
为直角三角形,求直线