题目内容
(本题满分14分).设数列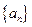 的前
的前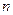 项和为
项和为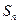 ,且
,且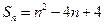 .
.
(1)求数列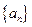 的通项公式;
的通项公式;
(2)设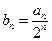 ,数列
,数列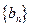 的前
的前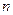 项和为
项和为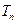 ,求证:
,求证: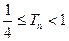 .
.
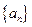 的前
的前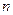 项和为
项和为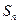 ,且
,且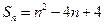 .
.(1)求数列
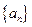 的通项公式;
的通项公式;(2)设
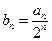 ,数列
,数列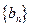 的前
的前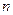 项和为
项和为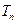 ,求证:
,求证: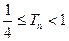 .
.(14分).解:当 时,
时, .
. …1分
…1分
当 时,
时,

 . ……3分
. ……3分
∵ 不适合上式,
不适合上式,
∴

 …4分
…4分
(2)证明: ∵ .
.
当 时,
时,

当 时,
时, , ①
, ①
 . ②
. ②
①-②得:


得 , ……8分
, ……8分
此式当 时也适合.
时也适合.
∴ N
N .
. 
∵ ,
,
∴ . ……10分
. ……10分
当 时,
时, ,
,
∴ . ……12分
. ……12分
∵ ,
,
∴ .
.
故 ,即
,即 .
.
综上, . ……………..14分
. ……………..14分
 时,
时, .
. …1分
…1分当
 时,
时,

 . ……3分
. ……3分∵
 不适合上式,
不适合上式,∴


 …4分
…4分(2)证明: ∵
 .
.当
 时,
时,

当
 时,
时, , ①
, ① . ②
. ②①-②得:


得
 , ……8分
, ……8分此式当
 时也适合.
时也适合.∴
 N
N .
. 
∵
 ,
,∴
 . ……10分
. ……10分当
 时,
时, ,
,∴
 . ……12分
. ……12分∵
 ,
,∴
 .
. 故
 ,即
,即 .
.综上,
 . ……………..14分
. ……………..14分 略

练习册系列答案
相关题目
 的公差大于0,且
的公差大于0,且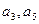 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且 .
. ,求数列
,求数列 的前
的前 项和
项和
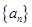 满足:
满足: 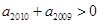 ,
,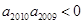 ,则使其前n
,则使其前n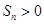 成立的最大自然数n是( ).
成立的最大自然数n是( ).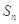 是等差数列
是等差数列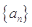 的前n项和,有
的前n项和,有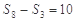 ,则
,则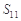 的值为( )
的值为( )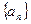 满足
满足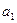 =-1,
=-1,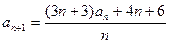 ,数列
,数列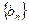 满足
满足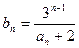
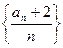 为等比数列,并求数列
为等比数列,并求数列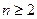 时,
时,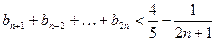
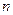 项和为
项和为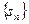 ,求证:当
,求证:当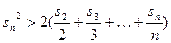 .
.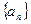 满足:
满足: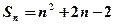 ,其中
,其中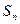 为数列
为数列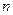 项和.
项和.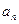 ;
;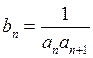 ,求
,求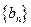 的前n项和Tn..
的前n项和Tn.. 中,
中, ,则等差数列
,则等差数列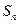 是公差不等于0的等差数列
是公差不等于0的等差数列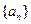 的前
的前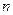
 项和,若
项和,若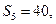 且
且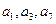 成等比
成等比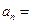 ___。
___。