题目内容
已知{e1 ,e2 ,e3} 为空间一基底,且以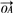 =e1+2e2-e3,
=e1+2e2-e3,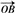 =-3e1+e2+2e3,
=-3e1+e2+2e3,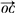 =e1+e2-e3,能否以
=e1+e2-e3,能否以 作为空间的一组基底?
作为空间的一组基底?
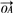 =e1+2e2-e3,
=e1+2e2-e3,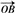 =-3e1+e2+2e3,
=-3e1+e2+2e3,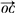 =e1+e2-e3,能否以
=e1+e2-e3,能否以 作为空间的一组基底?
作为空间的一组基底?解:假设 共面,则有
共面,则有
即e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)=(-3x+y)e1+(x+y)e2+(2x-y)e3.
∴ 此方程组无解,
此方程组无解,
 不共面,
不共面,
 可作为空间的一组基底.
可作为空间的一组基底.
 共面,则有
共面,则有
即e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)=(-3x+y)e1+(x+y)e2+(2x-y)e3.
∴
 此方程组无解,
此方程组无解, 不共面,
不共面, 可作为空间的一组基底.
可作为空间的一组基底.
练习册系列答案
相关题目
已知
,
是互相垂直的单位向量,
=λ
+
,
=
-2
,且
垂直,则下列各式正确的是( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a, |
| b |
| A、λ=1 | B、λ=2 |
| C、λ=3 | D、λ=4 |