题目内容

设 E1：
x2
a2
+
y2
b2
=1（其中a＞0）为焦点在（3，0），（-3，0）的椭圆；E2：焦点在（3，0）且准线为x=-3的抛物线．已知E1，E2的交点在直线x=3上，则 a=
 
．
分析：作出图形，如图，P到准线的距离是6，可求得PF1的长度，由勾股定理求得PF2，再由椭圆的定义求出椭圆的长轴即可求得a
解答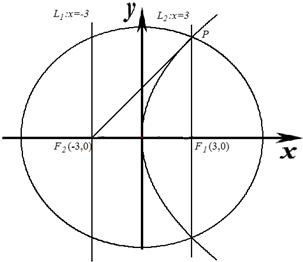：精英家教网解：设P为拋物线E1与椭圆E2的交点

P在E1上，根据拋物线的定义，d(P，L1)=
.
PF1
=6
P在E2上，根据椭圆的定义，
.
PF1
+
.
PF2
=2a?
.
PF2
=2a-6
∵P在直线x=3上，
∴
.
PF1
⊥x轴
故
.
PF2
2=
.
PF1
2+
.
F1F2
2?(2a-6)2=62+62?2a-6=±6
2
?a=3±3
2
(3-3
2
＜0，不合)
故答案为：3+3
2
．
点评：本题考查圆锥曲线的共同特征，解答本题关键是熟练掌握并会运用椭圆的定义以及抛物线的定义，理解图形中的垂直关系对解答本题也很重要．将题设中的位置关系转化成方程，考查了转化化归的思想．
练习册系列答案
相关题目
已知a＞b＞0，e1，e2分别是圆锥曲线
x2
a2
+
y2
b2
=1和
x2
a2
-
y2
b2
=1的离心率，设m=e1+e2，则m的取值范围是
 
．
如图，已知椭圆E1方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，圆E2方程为x2+y2=a2，过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C． 
（Ⅰ）若k1=1时，B恰好为线段AC的中点，试求椭圆E1的离心率e；
（Ⅱ）若椭圆E1的离心率e=
1
2
，F2为椭圆的右焦点，当|BA|+|BF2|=2a时，求k1的值；
（Ⅲ）设D为圆E2上不同于A的一点，直线AD的斜率为k2，当
k1
k2
=
b2
a2
时，试问直线BD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．
设双曲线
x2
a2
-
y2
b2
=1与-
x2
a2
+
y2
b2
=1(a＞0，b＞0)离心率分别为e1，e2，则当a，b变化时，e1+e2最小值为
2
2
2
2
．
（2007•河东区一模）已知：A、B是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的一条弦，向量
0A
+
OB
 交AB于点M，且向量
OM
=（2，1）．以M为焦点，以椭圆的右准线为相应准线的双曲线与直线AB交于点N（4，-1）．
（Ⅰ）求椭圆的离心率e1；
（Ⅱ）设双曲线的离心率为e2，若e1+e2=f（a），求 f（a） 的解析式，并确定它的定义域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网