题目内容
15．
如图是某几何体的三视图，正视图和侧视图都是等腰直角三角形，俯视图是边长为3的正方形，则此几何体的体积等于9．
分析 由已知中的三视图可得，该几何体是一个以俯视图为底面的四棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得，该几何体是一个以俯视图为底面的四棱锥，
其底面为边长为3的正方形，高为3，
故锥体的体积V=$\frac{1}{3}Sh$=$\frac{1}{3}$×3×3×3=9，
故答案为：9
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线的是某零件的三视图，则该零件的体积（单位：cm3）（ ）
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线的是某零件的三视图，则该零件的体积（单位：cm3）（ ）| A． | 40-5π | B． | 40-$\frac{5π}{2}$ | C． | 40-$\frac{4π}{3}$ | D． | 40-$\frac{2π}{3}$ |
20．一个几何体的三视图如图所示，图中直角三角形的直角边长均为1，则该几何体体积为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{{\sqrt{2}}}{6}$ | C． | $\frac{{\sqrt{3}}}{6}$ | D． | $\frac{1}{2}$ |
4．i是虚数单位，$\overrightarrow{z}$表示复数z的共轭复数，若$\overrightarrow{z}=1+i$，则$\frac{\overrightarrow{z}}{i}+i•z$=（ ）
| A． | -2 | B． | 2 | C． | -2i | D． | 2i |
7．
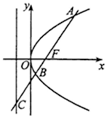如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）
如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）| A． | y2=3x | B． | y2=9x | C． | y2=$\frac{3}{2}$x | D． | y2=$\frac{9}{2}$x |