题目内容
已知向量
 ,函数
,函数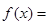
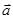 ·
· ,且最小正周期为
,且最小正周期为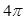 .
.
(1)求 的值;
的值;
(2)设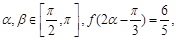
 ,求
,求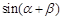 的值.
的值.
(1)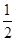 ;(2)
;(2)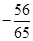 .
.
解析试题分析:(1)先由向量数量积的坐标表示,得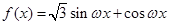 ,再由公式
,再由公式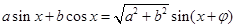 (其中
(其中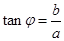 )简化得:
)简化得: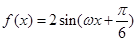 ,从而由最小正周期为
,从而由最小正周期为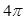 定出
定出 的值;(2)由
的值;(2)由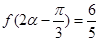 与
与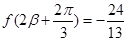 分别得到
分别得到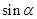 与
与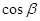 的值.再由
的值.再由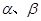 的范围及公式
的范围及公式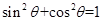 得到
得到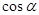 与
与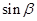 的值.最后代入公式
的值.最后代入公式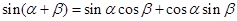 得到本题答案.在解题时注意由
得到本题答案.在解题时注意由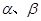 所在象限确定三角函数值的正负,而不能误以为有多种解.
所在象限确定三角函数值的正负,而不能误以为有多种解.
试题解析:(1)由已知,易得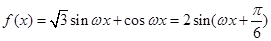 3分
3分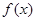 的最小正周期为
的最小正周期为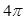 ,即
,即 ,解得
,解得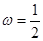 4分
4分
(2)由(1),知 ,则
,则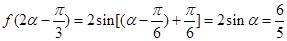 5分
5分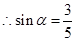 ,又
,又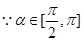 ,
,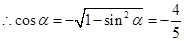 7分
7分
又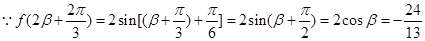 9分
9分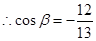 ,又
,又 ,
,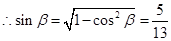 10分
10分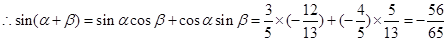 12分
12分
考点:1.平面向量的坐标运算;2.三角恒等变换;3.三角函数的基本运算.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
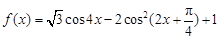 .
.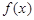 的最小正周期;
的最小正周期;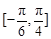 上的取值范围.
上的取值范围.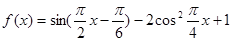 ,函数
,函数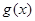 与函数
与函数 图像关于
图像关于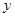 轴对称.
轴对称.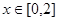 时,求
时,求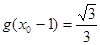 ,
,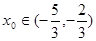 求
求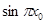 值.
值.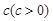 ,中心角
,中心角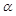 .求证:当
.求证:当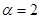 时该扇形面积最大;
时该扇形面积最大;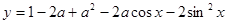
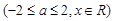 .求证:
.求证: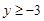 .
.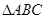 中,
中, ,
, ,
, .
. 的大小;
的大小; 的取值范围.
的取值范围.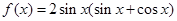 .
.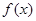 的最小正周期; (2)求
的最小正周期; (2)求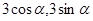 )
)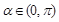 ,且
,且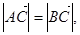 ,求
,求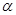 的大小;
的大小;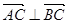 ,求
,求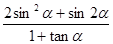 的值.
的值.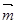
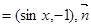
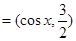 ,
,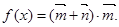
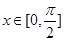 时,求函数
时,求函数 的值域:
的值域: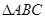 中,
中, 分别为角
分别为角 的对边,若
的对边,若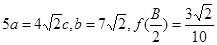 ,求边
,求边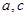 .
.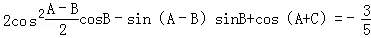
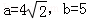 ,求向量
,求向量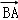 在
在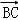 方向上的投影.
方向上的投影.