题目内容
已知动圆M过定点F(0,-
),且与直线y=
相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,
)在椭圆N上.
(1)求动圆圆心M的轨迹Γ的方程及椭圆N的方程;
(2)若动直线l与轨迹Γ在x=-4处的切线平行,且直线l与椭圆N交于B,C两点,试求当△ABC面积取到最大值时直线l的方程.
| 2 |
| 2 |
| 2 |
(1)求动圆圆心M的轨迹Γ的方程及椭圆N的方程;
(2)若动直线l与轨迹Γ在x=-4处的切线平行,且直线l与椭圆N交于B,C两点,试求当△ABC面积取到最大值时直线l的方程.
分析:(1)由抛物线定义得,点M的轨迹是以F(0,-
)为焦点,直线y=
为准线的抛物线,由此可得轨迹Γ的方程;设出椭圆方程,利用点A(1,
)在椭圆N上,可得椭圆N的方程;
(2)设出切线方程,代入椭圆方程,求得|BC|,点A到直线的距离,表示出面积,利用基本不等式,即可求得△ABC面积取到最大值时直线l的方程.
| 2 |
| 2 |
| 2 |
(2)设出切线方程,代入椭圆方程,求得|BC|,点A到直线的距离,表示出面积,利用基本不等式,即可求得△ABC面积取到最大值时直线l的方程.
解答:解:(1)过圆心M作直线y=
的垂线,垂足为H.
由题意得,|MH|=|MF|,由抛物线定义得,点M的轨迹是以F(0,-
)为焦点,直线y=
为准线的抛物线,
其方程为x2=-4
y.
设椭圆方程为
+
=1,将点A代入方程
+
=1
整理得a4-5a2+4=0,解得a2=4或a2=1(舍去)
故所求的椭圆方程为
+
=1;
(2)轨迹Γ的方程为x2=-4
y,即y=-
x2,则y′=-
x,所以轨迹轨迹Γ在x=-4处的切线斜率为k=
,
设直线l方程为y=
x+m,代入椭圆方程整理得4x2+2
mx+m2-4=0
因为△=8m2-16(m2-4)>0,解得-2<m<2;
设B(x1,y1),C(x2,y2),则x1+x2=-
m,x1x2=
所以BC|=
×
=
×
∵点A到直线的距离为d=
,所以S△ABC=
×
×
×
=
×
≤
当且仅当4-
m2=
m2,即m=±2时等号成立,此时直线l的方程为y=
x±2.
| 2 |
由题意得,|MH|=|MF|,由抛物线定义得,点M的轨迹是以F(0,-
| 2 |
| 2 |
其方程为x2=-4
| 2 |
设椭圆方程为
| y2 |
| a2 |
| x2 |
| a2-2 |
| 2 |
| a2 |
| 1 |
| a2-2 |
整理得a4-5a2+4=0,解得a2=4或a2=1(舍去)
故所求的椭圆方程为
| y2 |
| 4 |
| x2 |
| 2 |
(2)轨迹Γ的方程为x2=-4
| 2 |
| 1 | ||
4
|
| 1 | ||
2
|
| 2 |
设直线l方程为y=
| 2 |
| 2 |
因为△=8m2-16(m2-4)>0,解得-2<m<2;
设B(x1,y1),C(x2,y2),则x1+x2=-
| ||
| 2 |
| m2-4 |
| 4 |
所以BC|=
| 3 |
| (x1+x2)2-4x1x2 |
| 3 |
4-
|
∵点A到直线的距离为d=
| |m| | ||
|
| 1 |
| 2 |
| 3 |
4-
|
| |m| | ||
|
| ||
| 2 |
(4-
|
| 2 |
当且仅当4-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查三角形面积的计算,考查基本不等式的运用,正确表示三角形的面积是关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
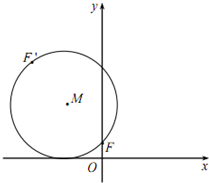 (2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
(2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.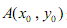 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q. 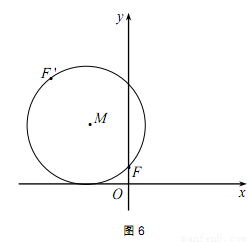
 ),且与直线y=
),且与直线y=