题目内容
(2012•珠海一模)已知函数g(x)=x2+2x,数列{an}满足a1=
,2an+1=g(an);数列{bn}的前n项和为Tn,数列{bn}的前n项积为Rn,bn=
(n∈N+).
(1)求证:2n+1Rn+Tn=2
(2)求证:5n-4n≤
<5n.
| 1 |
| 2 |
| 1 |
| 2+an |
(1)求证:2n+1Rn+Tn=2
(2)求证:5n-4n≤
| 5nTn |
| 2 |
分析:(1)先确定数列{bn}的通项,利用裂项法求和,利用叠乘法求积,即可证得结论;
(2)要证明5n-4n≤
<5n成立,只须证明2[1-(
)n]≤Tn<2成立.证明{an}是递增的正项数列,{bn}是递减的正项数列,即可证得结论.
(2)要证明5n-4n≤
| 5nTn |
| 2 |
| 4 |
| 5 |
解答:证明:(1)∵g(x)=x2+2x,∴2an+1=g(an)=
+2an
∴
=
•
=bn
∴bn=
•
=
•
=
•
=
-
∴Tn=b1+b2+b3+…+bn=(
-
)+(
-
)+(
-
)+…+(
-
)=2-
Rn=b1b2b3…bn=
•
•
•
…
=
•
=
∴2n+1Rn+Tn=2n+1•
+2-
=2
(2)要证明5n-4n≤
<5n成立,只须证明2[1-(
)n]≤Tn<2成立
由a1=
>0且an+1=
(
+2an)知,若an>0,则an+1>0
∴由(1)知Tn=2-
<2
又an+1-an=
>0,∴an+1>an>0,∴{an}是递增的正项数列
∴bn=
>
=bn+1>0,∴{bn}是递减的正项数列
∵b1=
=
,∴Rn=b1b2b3…bn≤(
)n
∵2n+1Rn+Tn=2,∴Tn=2-2n+1Rn≥2(1-2nRn)≥2[1-(
)n]
∴2[1-(
)n]≤Tn<2,
∴5n-4n≤
<5n
| a | 2 n |
∴
| 1 |
| 2+an |
| 1 |
| 2 |
| an |
| an+1 |
∴bn=
| 1 |
| 2 |
| an |
| an+1 |
| 1 |
| 2 |
| ||
| anan+1 |
| 1 |
| 2 |
| 2(an+1-an) |
| anan+1 |
| 1 |
| an |
| 1 |
| an+1 |
∴Tn=b1+b2+b3+…+bn=(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an+1 |
Rn=b1b2b3…bn=
| 1 |
| 2n |
| a1 |
| a2 |
| a2 |
| a3 |
| a3 |
| a4 |
| an |
| an+1 |
| 1 |
| 2n |
| a1 |
| an+1 |
| 1 |
| 2n+1an+1 |
∴2n+1Rn+Tn=2n+1•
| 1 |
| 2n+1an+1 |
| 1 |
| an+1 |
(2)要证明5n-4n≤
| 5nTn |
| 2 |
| 4 |
| 5 |
由a1=
| 1 |
| 2 |
| 1 |
| 2 |
| a | 2 n |
∴由(1)知Tn=2-
| 1 |
| an+1 |
又an+1-an=
| 1 |
| 2 |
| a | 2 n |
∴bn=
| 1 |
| 2+an |
| 1 |
| 2+an+1 |
∵b1=
| 1 |
| 2+a1 |
| 2 |
| 5 |
| 2 |
| 5 |
∵2n+1Rn+Tn=2,∴Tn=2-2n+1Rn≥2(1-2nRn)≥2[1-(
| 4 |
| 5 |
∴2[1-(
| 4 |
| 5 |
∴5n-4n≤
| 5nTn |
| 2 |
点评:本题考查数列递推式,考查裂项法与叠乘法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
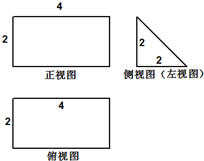 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知