题目内容
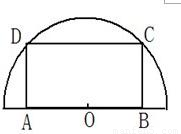
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.(1)怎样截取才能使截得的矩形ABCD的面积最大?并求最大面积;
(2)若将所截得的矩形铝皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形形罐子体积最大?并求最大面积.
【答案】分析:(1)【方法一】连接OC,设BC=x,矩形ABCD的面积为S;则S=AB•BC=2x =2
=2 ,由基本不等式可得S的最大值以及对应的x的取值;
,由基本不等式可得S的最大值以及对应的x的取值;
【方法二】连接OC,设∠BOC=θ,矩形ABCD的面积为S,则S=AB•BC=2OB•BC=900sin2θ,由三角函数的知识,得出S的最大值以及对应BC的值.
(2)【方法一】设圆柱底面半径为r,高为x,体积为V,由AB=2πr,得r,所以V=πr2h= (900x-x3);利用求导法,可得x=10
(900x-x3);利用求导法,可得x=10 时,V取最大值,为
时,V取最大值,为 ;
;
【方法二】连接OC,设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,则圆柱的底面半径为r= ,高h=30sinθ,所以V=πr2h=
,高h=30sinθ,所以V=πr2h= cos2θ=
cos2θ= (sinθ-sin3θ),用换元法,令t=sinθ,则V=
(sinθ-sin3θ),用换元法,令t=sinθ,则V= (t-t3),再由求导法,得t=
(t-t3),再由求导法,得t= 时,此时BC=10
时,此时BC=10 cm时,V取得最大值即可.
cm时,V取得最大值即可.
解答:解:如图所示,
(1)【方法一】连接OC,设BC=x,矩形ABCD的面积为S;则AB=2 (其中0<x<30),
(其中0<x<30),
∴S=2x =2
=2 ≤x2+(900-x2)=900,当且仅当x2=900-x2,即x=15
≤x2+(900-x2)=900,当且仅当x2=900-x2,即x=15 时,S取最大值900;
时,S取最大值900;
所以,取BC= cm时,矩形ABCD的面积最大,最大值为900cm2.
cm时,矩形ABCD的面积最大,最大值为900cm2.
【方法二】连接OC,设∠BOC=θ,矩形ABCD的 面积为S,则BC=30sinθ,OB=30cosθ(其中0<θ< );
);
∴S=AB•BC=2OB•BC=900sin2θ,且当sin2θ=1,即θ= 时,S取最大值为900,此时BC=15
时,S取最大值为900,此时BC=15 ;
;
所以,取BC=15 时,矩形ABCD的面积最大,最大值为900cm2.
时,矩形ABCD的面积最大,最大值为900cm2.
(2)【方法一】设圆柱底面半径为r,高为x,体积为V,由AB=2 =2πr,得r=
=2πr,得r= ,
,
∴V=πr2h= (900x-x3),(其中0<x<30);由V′=
(900x-x3),(其中0<x<30);由V′= (900-3x2)=0,得x=10
(900-3x2)=0,得x=10 ;
;
因此V= (900x-x3)在
(900x-x3)在 上是增函数,在(10
上是增函数,在(10 ,30)上是减函数;
,30)上是减函数;
∴当x=10 时,V的最大值为
时,V的最大值为 ,即取BC=10
,即取BC=10 cm时,做出的圆柱形罐子体积最大,最大值为
cm时,做出的圆柱形罐子体积最大,最大值为 cm3.
cm3.
【方法二】连接OC,设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,
则圆柱的底面半径为r= ,高h=30sinθ,(其中0<θ<
,高h=30sinθ,(其中0<θ< ),
),
所以V=πr2h= cos2θ=
cos2θ= (sinθ-sin3θ),
(sinθ-sin3θ),
设t=sinθ,则V= (t-t3),由V′=
(t-t3),由V′= (1-3t2)=0,得t=
(1-3t2)=0,得t= ,
,
因此V= (t-t3)在(0,
(t-t3)在(0, )上是增函数,在(
)上是增函数,在( ,1)上是减函数;
,1)上是减函数;
所以,当t= 时,即sinθ=
时,即sinθ= ,此时BC=10
,此时BC=10 cm时,V有最大值,为
cm时,V有最大值,为 cm3.
cm3.
点评:本题综合考查了二次函数,三次函数的最值问题,这里应用了基本不等式,以及求导数的方法求出了函数的最值.
 =2
=2 ,由基本不等式可得S的最大值以及对应的x的取值;
,由基本不等式可得S的最大值以及对应的x的取值;【方法二】连接OC,设∠BOC=θ,矩形ABCD的面积为S,则S=AB•BC=2OB•BC=900sin2θ,由三角函数的知识,得出S的最大值以及对应BC的值.
(2)【方法一】设圆柱底面半径为r,高为x,体积为V,由AB=2πr,得r,所以V=πr2h=
 (900x-x3);利用求导法,可得x=10
(900x-x3);利用求导法,可得x=10 时,V取最大值,为
时,V取最大值,为 ;
;【方法二】连接OC,设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,则圆柱的底面半径为r=
 ,高h=30sinθ,所以V=πr2h=
,高h=30sinθ,所以V=πr2h= cos2θ=
cos2θ= (sinθ-sin3θ),用换元法,令t=sinθ,则V=
(sinθ-sin3θ),用换元法,令t=sinθ,则V= (t-t3),再由求导法,得t=
(t-t3),再由求导法,得t= 时,此时BC=10
时,此时BC=10 cm时,V取得最大值即可.
cm时,V取得最大值即可.解答:解:如图所示,

(1)【方法一】连接OC,设BC=x,矩形ABCD的面积为S;则AB=2
 (其中0<x<30),
(其中0<x<30),∴S=2x
 =2
=2 ≤x2+(900-x2)=900,当且仅当x2=900-x2,即x=15
≤x2+(900-x2)=900,当且仅当x2=900-x2,即x=15 时,S取最大值900;
时,S取最大值900;所以,取BC=
 cm时,矩形ABCD的面积最大,最大值为900cm2.
cm时,矩形ABCD的面积最大,最大值为900cm2.【方法二】连接OC,设∠BOC=θ,矩形ABCD的 面积为S,则BC=30sinθ,OB=30cosθ(其中0<θ<
 );
);∴S=AB•BC=2OB•BC=900sin2θ,且当sin2θ=1,即θ=
 时,S取最大值为900,此时BC=15
时,S取最大值为900,此时BC=15 ;
;所以,取BC=15
 时,矩形ABCD的面积最大,最大值为900cm2.
时,矩形ABCD的面积最大,最大值为900cm2.(2)【方法一】设圆柱底面半径为r,高为x,体积为V,由AB=2
 =2πr,得r=
=2πr,得r= ,
,∴V=πr2h=
 (900x-x3),(其中0<x<30);由V′=
(900x-x3),(其中0<x<30);由V′= (900-3x2)=0,得x=10
(900-3x2)=0,得x=10 ;
;因此V=
 (900x-x3)在
(900x-x3)在 上是增函数,在(10
上是增函数,在(10 ,30)上是减函数;
,30)上是减函数;∴当x=10
 时,V的最大值为
时,V的最大值为 ,即取BC=10
,即取BC=10 cm时,做出的圆柱形罐子体积最大,最大值为
cm时,做出的圆柱形罐子体积最大,最大值为 cm3.
cm3.【方法二】连接OC,设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,
则圆柱的底面半径为r=
 ,高h=30sinθ,(其中0<θ<
,高h=30sinθ,(其中0<θ< ),
),所以V=πr2h=
 cos2θ=
cos2θ= (sinθ-sin3θ),
(sinθ-sin3θ),设t=sinθ,则V=
 (t-t3),由V′=
(t-t3),由V′= (1-3t2)=0,得t=
(1-3t2)=0,得t= ,
,因此V=
 (t-t3)在(0,
(t-t3)在(0, )上是增函数,在(
)上是增函数,在( ,1)上是减函数;
,1)上是减函数;所以,当t=
 时,即sinθ=
时,即sinθ= ,此时BC=10
,此时BC=10 cm时,V有最大值,为
cm时,V有最大值,为 cm3.
cm3.点评:本题综合考查了二次函数,三次函数的最值问题,这里应用了基本不等式,以及求导数的方法求出了函数的最值.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
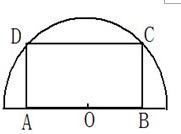 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.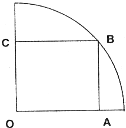 如图,在半径为30cm的
如图,在半径为30cm的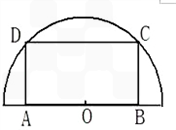
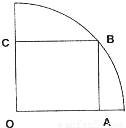
 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xcm,圆柱的体积为Vcm3.
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xcm,圆柱的体积为Vcm3.