题目内容
已知两点 到直线
到直线 的距离分别为
的距离分别为 ,则满足条件的直线
,则满足条件的直线 共有( )条
共有( )条
 到直线
到直线 的距离分别为
的距离分别为 ,则满足条件的直线
,则满足条件的直线 共有( )条
共有( )条| A.1 | B.2 | C.3 | D.4 |
C
试题分析:由A和B的坐标,利用两点间的距离公式求出|AB|的长,然后以A为圆心,
 为半径画圆A,以B为圆心
为半径画圆A,以B为圆心 为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。
为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。解:∵A(1,2),B(3,1),∴|AB|=
 ,分别以A,B为圆心,
,分别以A,B为圆心, ,
, 为半径作两个圆,如图所示:
为半径作两个圆,如图所示:
即d=R+r,∴两圆外切,有三条共切线,则满足条件的直线l共有3条.故选C
点评:此题考查了圆与圆位置关系的判定,以及直线与圆的位置关系,圆与圆位置关系由R,r及d间的关系来判定,当d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R-r时,两圆外离,解题的关键是根据题意画出相应的图形,找出两圆的公切线的条数即为所求直线l的条数

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与圆
与圆 相切,则实数
相切,则实数 等于( )
等于( ) 或
或


 相切的直线与
相切的直线与 轴,
轴,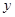 轴的正半轴交于A、B且
轴的正半轴交于A、B且 ,则三角形AOB面积的最小值为 。
,则三角形AOB面积的最小值为 。 :
: 的圆心到直线3x+4y+14=0的距离是 .
的圆心到直线3x+4y+14=0的距离是 .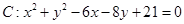 ,直线
,直线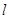 过定点
过定点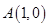 .
.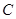 的坐标和圆的半径
的坐标和圆的半径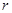 ;
;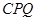 面积的最大值,并求此时
面积的最大值,并求此时 轴截得的弦长等于 。
轴截得的弦长等于 。 所表示的圆有最大的面积,则直线
所表示的圆有最大的面积,则直线 的倾斜角
的倾斜角 =_________ .
=_________ . 的点数共有______ 个。
的点数共有______ 个。