题目内容
已知函数![]() ,
,![]() ,
,![]() 为正的常数.
为正的常数.
(1)求函数![]() 的定义域;
的定义域;
(2)求![]() 的单调区间,并指明单调性;
的单调区间,并指明单调性;
(3)若![]() ,
,![]() ,证明:
,证明:![]() .
.
(1)![]() (2)
(2)![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.(3)略
上为减函数.(3)略
解析:
(1)∵![]() 的定义域为
的定义域为![]() , …………1分
, …………1分
![]() 有意义,则
有意义,则![]() 那么
那么![]() 的定义域为
的定义域为![]() .
.
………… 3分
(2)![]() ,
,
则![]() , ………… 5分
, ………… 5分
由![]() ,得
,得![]() ,解得
,解得![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数. ………… 7分
上为减函数. ………… 7分
(3)要证![]() ,
,
只须证![]() .
.
而在(2)中,取![]() ,则
,则![]() ,………… 9分
,………… 9分
则![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
∴![]() 的最小值为
的最小值为![]()
![]() .
.
那么![]() ,得
,得
![]() ,
,
即![]() . ………… 12分
. ………… 12分

练习册系列答案
相关题目
 (
( 均为正常数),设函数
均为正常数),设函数 在
在 处有极值.
处有极值. ,不等式
,不等式 总成立,求实数
总成立,求实数 的取值范围;
的取值范围; 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. ,其中
,其中 为正常数.
为正常数. 在
在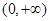 上的最大值;
上的最大值; 满足:
满足: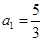 ,
, ,
,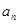 ;
; ,
, ;
; .
.