题目内容
已知:关于x的方程2x2-(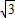 +1)x+m=0的两根为sinθ和cosθ,θ∈(0,2π).求:
+1)x+m=0的两根为sinθ和cosθ,θ∈(0,2π).求:(1)
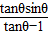 +
+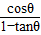 的值;
的值;(2)m的值;
(3)方程的两根及此时θ的值.
【答案】分析:(1)由题意得 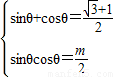 ,再根据三角函数的恒等变换化简
,再根据三角函数的恒等变换化简 +
+ 为 sinθ+cosθ,从而求得结果.
为 sinθ+cosθ,从而求得结果.
(2)由sinθ+cosθ=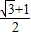 、sinθcosθ=
、sinθcosθ=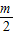 以及同角三角函数的基本关系可得 1+m=
以及同角三角函数的基本关系可得 1+m=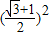 ,由此解得 m的值.
,由此解得 m的值.
(3)由以上可得,sinθ+cosθ=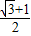 、sinθcosθ=
、sinθcosθ= ,解得 sinθ 和cosθ 的值,从而求得故此时方程的两个根及θ的值.
,解得 sinθ 和cosθ 的值,从而求得故此时方程的两个根及θ的值.
解答:解:(1)由于关于x的方程2x2-( +1)x+m=0的两根为sinθ和cosθ,故有
+1)x+m=0的两根为sinθ和cosθ,故有 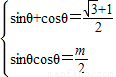 ,
,
∴ +
+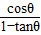 =
= +
+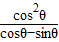 =
=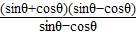 =sinθ+cosθ=
=sinθ+cosθ=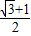 .
.
(2)由sinθ+cosθ=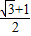 、sinθcosθ=
、sinθcosθ= ,∴sin2θ+2sinθcosθ+cos2θ=
,∴sin2θ+2sinθcosθ+cos2θ=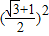 ,即 1+m=
,即 1+m= ,解得 m=
,解得 m=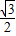 .
.
(3)由以上可得,sinθ+cosθ=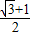 、sinθcosθ=
、sinθcosθ= ,解得 sinθ=
,解得 sinθ= ,cosθ=
,cosθ= ; 或者 sinθ=
; 或者 sinθ= ,cosθ=
,cosθ= .
.
故此时方程的两个根分别为 、
、 ,对应θ的值为
,对应θ的值为 或
或 .
.
点评:本题主要考查一元二次方程根与系数的关系,同角三角函数的基本关系的应用,三角函数的恒等变换,根据三角函数的值求角,属于中档题.
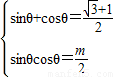 ,再根据三角函数的恒等变换化简
,再根据三角函数的恒等变换化简 +
+ 为 sinθ+cosθ,从而求得结果.
为 sinθ+cosθ,从而求得结果.(2)由sinθ+cosθ=
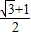 、sinθcosθ=
、sinθcosθ=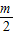 以及同角三角函数的基本关系可得 1+m=
以及同角三角函数的基本关系可得 1+m=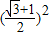 ,由此解得 m的值.
,由此解得 m的值.(3)由以上可得,sinθ+cosθ=
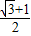 、sinθcosθ=
、sinθcosθ= ,解得 sinθ 和cosθ 的值,从而求得故此时方程的两个根及θ的值.
,解得 sinθ 和cosθ 的值,从而求得故此时方程的两个根及θ的值.解答:解:(1)由于关于x的方程2x2-(
 +1)x+m=0的两根为sinθ和cosθ,故有
+1)x+m=0的两根为sinθ和cosθ,故有 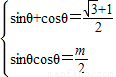 ,
,∴
 +
+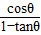 =
= +
+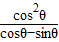 =
=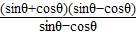 =sinθ+cosθ=
=sinθ+cosθ=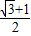 .
.(2)由sinθ+cosθ=
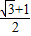 、sinθcosθ=
、sinθcosθ= ,∴sin2θ+2sinθcosθ+cos2θ=
,∴sin2θ+2sinθcosθ+cos2θ=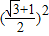 ,即 1+m=
,即 1+m= ,解得 m=
,解得 m=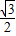 .
.(3)由以上可得,sinθ+cosθ=
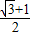 、sinθcosθ=
、sinθcosθ= ,解得 sinθ=
,解得 sinθ= ,cosθ=
,cosθ= ; 或者 sinθ=
; 或者 sinθ= ,cosθ=
,cosθ= .
.故此时方程的两个根分别为
 、
、 ,对应θ的值为
,对应θ的值为 或
或 .
.点评:本题主要考查一元二次方程根与系数的关系,同角三角函数的基本关系的应用,三角函数的恒等变换,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目