题目内容
已知:关于x的方程2x2+kx-1=0(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是-1,求另一个根及k值.
分析:(1)方程有两个不相等的实数根?△≥0,故只需求出△,判断△≥0恒成立即可.
(2)方程的一个根是-1,将x=-1代入到方程中即可求出k,由维达定理即可求出另一个根.
(2)方程的一个根是-1,将x=-1代入到方程中即可求出k,由维达定理即可求出另一个根.
解答:解:(1)证明:2x2+kx-1=0,△=k2-4×2×(-1)=k2+8,
无论k取何值,k2≥0,所以k2+8>0,即△>0,∴方程2x2+kx-1=0有两个不相等的实数根.
(2)设2x2+kx-1=0的另一个根为x,
则x-1=-
,(-1)•x=-
,
解得:x=
,k=1,∴2x2+kx-1=0的另一个根为
,k的值为1.
无论k取何值,k2≥0,所以k2+8>0,即△>0,∴方程2x2+kx-1=0有两个不相等的实数根.
(2)设2x2+kx-1=0的另一个根为x,
则x-1=-
| k |
| 2 |
| 1 |
| 2 |
解得:x=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查二次方程的根的问题、二次方程根和系数的关系,属基础知识的考查.

练习册系列答案
相关题目
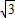 +1)x+m=0的两根为sinθ和cosθ,θ∈(0,2π).求:
+1)x+m=0的两根为sinθ和cosθ,θ∈(0,2π).求: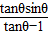 +
+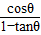 的值;
的值;