题目内容
12．在Rt△ABC中，D是斜边AB的中点，AC=6，BC=8，EC⊥平面ABC，且EC=12，则ED=13．分析 由EC垂直Rt△ABC的两条直角边，可知EC⊥面ABC，再根据D是斜边AB的中点，AC=6，BC=8，可求得CD的长，根据勾股定理可求得DE的长．
解答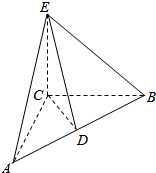 
解：如图，EC⊥面ABC，
而CD?面ABC，
∴EC⊥CD，
∵AC=6，BC=8，EC=12，△ABC是直角三角形，D是斜边AB的中点，
∴CD=5，ED=$\sqrt{E{C}^{2}+C{D}^{2}}$=13．
故答案为：13．
点评 本题主要考查了线面垂直的判定和性质定理，利用勾股定理求线段的长度，考查了空间想象能力和推理论证能力，属于基本知识的考查．
练习册系列答案
口算题天天练系列答案
相关题目
3．在建立两个变量y与x的回归模型中，分别选择了4个不同模型，模型1、2、3、4的R2分别为0.99、0.89、0.52、0.16，则其中拟合得最好得模型是（ ）
| A． | 模型1 | B． | 模型2 | C． | 模型3 | D． | 模型4 |
如图，在平行六面体ABCD-A1B1C1D1中，M，N分别是C1D1，AB的中点，E在AA1上且AE=2EA1，F在CC1上且CF=$\frac{1}{2}$FC1，判断$\overrightarrow{ME}$与$\overrightarrow{NF}$是否共线？
如图，已知P为x轴正半轴上的动点，Q为射线y=$\sqrt{3}$x（x＞0）上的动点，△POQ的面积为8，求线段PQ的中心R的轨迹的参数方程．
1．设a＞b＞0，则下列关系式成立的是（ ）
| A． | aabb＞（ab）${\;}^{\frac{a+b}{2}}$ | B． | aabb＜（ab）${\;}^{\frac{a+b}{2}}$ | ||
| C． | aabb=（ab）${\;}^{\frac{a+b}{2}}$ | D． | aabb与（ab）${\;}^{\frac{a+b}{2}}$的大小不能确定 |