题目内容

过抛物线y²=2px（p＞0）的焦点F的直线l与抛物线在第一象限的交点为A，直线l与抛物线的准线的交点为B，点A在抛物线的准线上的射影为C，若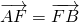 $数学公式$ ， $数学公式$ ，则抛物线的方程为

A.
y²=6x
B.
y²=3x
C.
y²=12x
D.
$数学公式$

D
分析：设抛物线的准线与x轴的交点为D，F为线段AB的中点，进而可知|AF|和|AB|，推断出AF|= $\text{[math]}$ |AB|，求得∠ABC，进而根据 $\text{[math]}$ ，求得p，则抛物线方程可得．
解答：设抛物线的准线与x轴的交点为D，
依题意，F为线段AB的中点，故|AF|=|AC|=2|FD|=2p，
|AB|=2|AF|=2|AC|=4p，
∴∠ABC=30°，| $\text{[math]}$ |=2 $\text{[math]}$ p， $\text{[math]}$ =4p×2 $\text{[math]}$ pcos30°=36，
解得p= $\text{[math]}$ ，
∴抛物线的方程为y²=2 $\text{[math]}$ x．
故选D．
点评：本题主要考查了抛物线的标准方程，考查抛物线的基础知识，考查数形结合思想．

练习册系列答案

举一反三同步巧讲精练系列答案

口算与应用题卡系列答案

培优新题库系列答案

教材备考笔记系列答案

竖式计算卡系列答案

名师点睛字词句段篇系列答案

名校直通车系列答案

初中学业水平考查系列答案

实验活动练习册系列答案

题优讲练测系列答案

相关题目

过抛物线y²=2px（p＞0）的焦点F的直线l与抛物线在第一象限的交点为A，与抛物线的准线的交点为B，点A在抛物线准线上的射影为C，若

=48，则抛物线的方程为（　　）

过抛物线y2=2px（p＞0）上一定点P（x₀，y₀）（y₀＞0）作两条直线分别交抛物线于A（x₁，y₁），B（x₂，y₂），若PA与PB的斜率存在且倾斜角互补，则

过抛物线y²=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为抛物线的顶点．则△ABO是一个（　　）

A、等边三角形

B、直角三角形

C、不等边锐角三角形

D、钝角三角形

过抛物线y²=2px（p＞0）的焦点F的直线AB交抛物线于A，B两点，弦AB的中点为M，过M作AB的垂直平分线交x轴于N．
（1）求证：FN=

AB；
（2）过A，B的抛物线的切线相交于P，求P的轨迹方程．

（2010•武汉模拟）已知过抛物线y²=2px（p＞0）的焦点F的直线交抛物线于M、N两点，直线OM、ON（O为坐标原点）分别与准线l：x=-

相交于P、Q两点，则∠PFQ=（　　）