题目内容
如果在（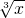
+
）n的展开式中，二项式系数之和为256，那么展开式中的常数项是 ________．
7
分析：根据所给的二项式系数之和为256，得到n的值，写出二项式的通项，因为要求常数项，所以使得通项式的x的指数是0，得到r的值，把r的值代入前面所写的通项，得到展开式中的常数项．
解答：∵在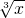（+）n的展开式中，二项式系数之和是2n
∵二项式系数之和为256，
∴2n=256，
∴n=8
∴Tr+1=
，
∵
=0
∴r=2
∴展开式中的常数项是
=7．
故答案为：7
点评：本题是一个二项展开式的特挣项的求法．还考到二项式系数之和的特点，解本题时容易公式记不清楚导致计算错误，所以牢记公式．它是经常出现的一个客观题．
分析：根据所给的二项式系数之和为256，得到n的值，写出二项式的通项，因为要求常数项，所以使得通项式的x的指数是0，得到r的值，把r的值代入前面所写的通项，得到展开式中的常数项．
解答：∵在（
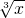+）n的展开式中，二项式系数之和是2n∵二项式系数之和为256，
∴2n=256，
∴n=8
∴Tr+1=
，∵
=0∴r=2
∴展开式中的常数项是
=7．故答案为：7
点评：本题是一个二项展开式的特挣项的求法．还考到二项式系数之和的特点，解本题时容易公式记不清楚导致计算错误，所以牢记公式．它是经常出现的一个客观题．
练习册系列答案
英才计划期末调研系列答案
相关题目
（2010•福建模拟）如图，正方体ABCD-A1B1C1D1中，M、N分别为AB、BC的中点．
