Question

【题目】已知圆，为坐标原点，动点在圆外，过点作圆的切线，设切点为.

（1）若点运动到处，求此时切线的方程；

（2）求满足的点的轨迹方程.

Answer 1

【答案】（1）或； （2）.

【解析】

试题分析：（1）当过点P的切线斜率存在时，由点斜式设出切线方程，再利用圆心到切线的距离等于半径求得k的值，可得切线方程．当切线斜率不存在时，要检验是否满足条件，从而得出结论． （2）设点，由圆的切线的性质知，为直角三角形，可得，；由，化简可得点P的轨迹方程为.

试题解析：

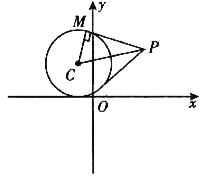
解: 把圆C的方程化为标准方程为（x＋1）2＋（y－2）2＝4，

∴圆心为C（－1,2），半径r＝2.

（1）当l的斜率不存在时，此时l的方程为x＝1，C到l的距离d＝2＝r，满足条件．

当l的斜率存在时，设斜率为k，得l的方程为y－3＝k（x－1），即kx－y＋3－k＝0，

则＝2，解得k＝.

∴l的方程为y－3＝（x－1），

即3x＋4y－15＝0.

综上，满足条件的切线l的方程为或.

（2）设P（x，y），则|PM|2＝|PC|2－|MC|2＝（x＋1）2＋（y－2）2－4，

|PO|2＝x2＋y2，

∵|PM|＝|PO|.

∴（x＋1）2＋（y－2）2－4＝x2＋y2，

整理，得2x－4y＋1＝0，

∴点P的轨迹方程为.