Question

【题目】某海轮以30海里/小时的速度航行，在A点测得海面上油井P在南偏东60°，向北航行40分钟后到达B点，测得油井P在南偏东30°，海轮改为北偏东60°的航向再行驶80分钟到达C点，求P、C间的距离（ ）海里.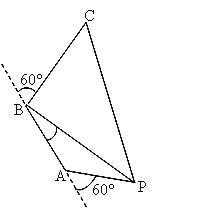
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解答：如图，在△ABP中，AB = 30× = 20， ∠APB =30°，∠BAP =120°，
由正弦定理，得： ，即 ，解得BP = .
在△BPC中，BC = 30× = 40，
由已知∠PBC =90°，∴PC = (海里).
所以P、C间的距离为 海里.
分析：本题主要考查了正弦定理在解三角形中的应用，解决实际问题的关键是要把实际问题转化为数学问题，然后利用数学知识进行求解.