题目内容
已知数列{ }的前n项和
}的前n项和 (n为正整数)。
(n为正整数)。
(I)令 ,求证数列{
,求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;
(Ⅱ)令 ,
, 试比较
试比较 与
与 的大小,并予以证明.
的大小,并予以证明.



由①-②得
 ………………………9
………………………9
 ……………………………………11
……………………………………11
于是确定 的大小关系等价于比较
的大小关系等价于比较 的大小
的大小
 ......
......
猜想:当 证明如下:
证明如下:
证法1:(1)当n=3时,由猜想显然成立.
(2)假设 时猜想成立.即
时猜想成立.即
则 时,
时,
所以当 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切 的正整数,都有
的正整数,都有
证法2:当 时
时

综上所述,当
 ,当
,当 时
时 ………………………12
………………………12

练习册系列答案
相关题目
 ,
, 轴在地平面上,
轴在地平面上, 轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程 表示的曲线上,其中
表示的曲线上,其中 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标. 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
 内角
内角 的对边分别为
的对边分别为 ,且满足
,且满足
 .
. 及直线
及直线 截圆C所得的弦长均为10,则圆C的面积是 .
截圆C所得的弦长均为10,则圆C的面积是 .  的展开式中含
的展开式中含 项,则最小自然数
项,则最小自然数 是( )
是( )  ,
, ,函数
,函数 若
若 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D. 
 ,则 ( )
,则 ( ) B.
B. C.
C. D.
D.
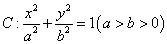 的离心率为
的离心率为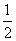 ,以原点为圆心,椭圆的短半轴长为
,以原点为圆心,椭圆的短半轴长为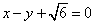 相切.
相切.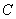 的方程;
的方程;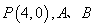 是椭圆
是椭圆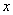 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接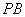 交椭圆
交椭圆 ,证明:直线
,证明:直线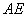 与
与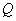 ;
;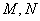 两点,求
两点,求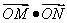 的取值范围.
的取值范围.