题目内容
设P < 0 是一常数,过点 `Q(2P,0)的直线与抛物线
`Q(2P,0)的直线与抛物线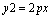 交于相导两点A、B 以线段AB 为直径
交于相导两点A、B 以线段AB 为直径 作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.
作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.

满足
 消去x得
消去x得
 ,由此得
,由此得


因此
在圆H的圆周上.

 故|OH|为上面圆的半径R,从而以AB
故|OH|为上面圆的半径R,从而以AB
为直径直圆必过点O(0,0).又 
 J最小.从而圆的面积最小,此时直
J最小.从而圆的面积最小,此时直


练习册系列答案
相关题目
题目内容
设P < 0 是一常数,过点 `Q(2P,0)的直线与抛物线
`Q(2P,0)的直线与抛物线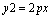 交于相导两点A、B 以线段AB 为直径
交于相导两点A、B 以线段AB 为直径 作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.
作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求圆H的面积最小时直线AB的方程.

满足
 消去x得
消去x得
 ,由此得
,由此得


因此
在圆H的圆周上.

 故|OH|为上面圆的半径R,从而以AB
故|OH|为上面圆的半径R,从而以AB
为直径直圆必过点O(0,0).又 
 J最小.从而圆的面积最小,此时直
J最小.从而圆的面积最小,此时直

