题目内容
【题目】设函数![]() .
.
(Ⅰ)证明:当![]() 时,
时,![]() ;
;
(Ⅱ)设当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
试题(Ⅰ)在证明不等式时一般可以通过等价变形将要证明的不等式简化,本题中注意到![]() 时,
时,![]() ,于是有
,于是有![]() ,即
,即![]() 令
令![]() 只需证明
只需证明![]() 即可;(Ⅱ)由
即可;(Ⅱ)由![]() 时,
时,![]() 恒成立,故
恒成立,故![]() .
.
设![]() ,
,![]() ,
,![]()
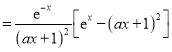 .
.
设![]() ,
,![]() ,则
,则![]() .
.![]() 当
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() ,故
,故![]() .所以
.所以![]() 单调递增,
单调递增,![]() ,故
,故![]() 单调递增,
单调递增,![]() 恒成立,符合题意.当
恒成立,符合题意.当![]() ,即
,即![]() 时,存在
时,存在![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,与
,与![]() 恒成立矛盾.
恒成立矛盾.
试题解析:(Ⅰ)证明:注意到![]() 时,
时,![]() ,
,
于是有![]() ,即
,即![]() .
.
令![]() ,
,![]() .
.![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
可见![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,
![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() ,从而
,从而![]() ,且当且仅当
,且当且仅当![]() 时等号成立.
时等号成立.
(Ⅱ)解:由![]() 时,
时,![]() 恒成立,故
恒成立,故![]() .
.
设![]() ,
,![]() ,
,
则![]()
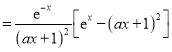 .
.
设![]() ,
,![]() ,
,
则![]() .
.![]()
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() ,故
,故![]() .
.
所以![]() 单调递增,
单调递增,![]() ,故
,故![]() 单调递增,
单调递增,![]() 恒成立,符合题意.
恒成立,符合题意.
当![]() ,即
,即![]() 时,存在
时,存在![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,与
,与![]() 恒成立矛盾.
恒成立矛盾.
综合上述得实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目