题目内容
方程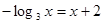 的根所在的区间为 ( )
的根所在的区间为 ( )
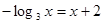 的根所在的区间为 ( )
的根所在的区间为 ( ) | A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
A
试题分析:令
 ,因为
,因为
又
 在
在 ,
, ,所以
,所以 在(0,1)内有零点,即方程
在(0,1)内有零点,即方程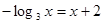 的根所在的区间为(0,1)。
的根所在的区间为(0,1)。点评:方程的根、对应函数的零点、函数的图像与x轴交点的横坐标三者是等价的。

练习册系列答案
相关题目
题目内容
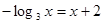 的根所在的区间为 ( )
的根所在的区间为 ( ) | A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
 ,因为
,因为
 在
在 ,
, ,所以
,所以 在(0,1)内有零点,即方程
在(0,1)内有零点,即方程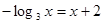 的根所在的区间为(0,1)。
的根所在的区间为(0,1)。