题目内容
(本题满分12分)定义在R上的偶函数 满足,
满足, 时,
时, 。
。
(1)求 时,
时, 的解析式;
的解析式;
(2)求证:函数 在区间
在区间 上递减。
上递减。
 满足,
满足, 时,
时, 。
。(1)求
 时,
时, 的解析式;
的解析式;(2)求证:函数
 在区间
在区间 上递减。
上递减。 解:(1) 时,
时, ;(2)
;(2) 在
在 上递减。
上递减。
 时,
时, ;(2)
;(2) 在
在 上递减。
上递减。本小题主要考查函数单调性的应用、函数奇偶性的应用、函数的值域等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题
1)欲求x<0时的解析式,根据偶函数f(x)的性质,先设x<0时,f(x)=f(-x)即可求得;
(2)利用函数单调性的定义证明,任取x1,x2∈(0,2)且x1<x2,作差f(x1)-f(x2)与0比较即可
解:(1) 时,
时, ;
;
(2)任取 且
且 ,∵
,∵
而 ,
, ,∴
,∴ ,即
,即 ,
,
∴ 在
在 上递减。
上递减。
1)欲求x<0时的解析式,根据偶函数f(x)的性质,先设x<0时,f(x)=f(-x)即可求得;
(2)利用函数单调性的定义证明,任取x1,x2∈(0,2)且x1<x2,作差f(x1)-f(x2)与0比较即可
解:(1)
 时,
时, ;
;(2)任取
 且
且 ,∵
,∵
而
 ,
, ,∴
,∴ ,即
,即 ,
,∴
 在
在 上递减。
上递减。 
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
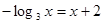 的根所在的区间为 ( )
的根所在的区间为 ( ) 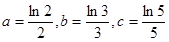 ,则【 】
,则【 】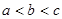
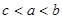
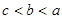
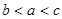
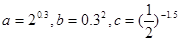 ,则
,则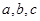 的大小关系是( )
的大小关系是( )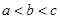
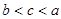
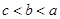
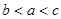
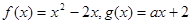 ,对任意的
,对任意的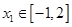 ,都存在
,都存在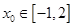 ,使得
,使得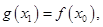 则实数
则实数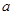 的取值范围是______________.
的取值范围是______________. 若关于x的方程
若关于x的方程 有三个不同的实数解
有三个不同的实数解 ,
, ,
, ,且
,且 ,则下列结论错误的是
,则下列结论错误的是



 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为  (
( 且
且 )
)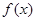 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值; 的图象,写函数
的图象,写函数 ,如果方程
,如果方程 至少有一个根
至少有一个根 ,就称方程为合格方程,则合格方程的个数为( )
,就称方程为合格方程,则合格方程的个数为( )