题目内容
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.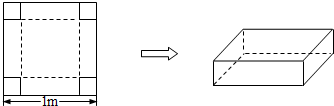

长方体的底面正方形的边长为1-2x,高为x,所以,容积V=4(x-
)2x,
铁皮箱的高度x与底面正方形的边长1-2x的比值
≤c,得 0<x≤
,
由均值不等式知V=2(
-x)(
-x)(2x)≥
,
当
-x=2x,即x=
时等号成立.
①当
≤
,即 c≥
,Vmax=
;
②当
≤
,即 0<c<
时,V'(x)=12(x-
) 2-
,
则V′(x)在(0,
)上单调递减,
∴V'(x)≥V'(
)>V'(
)=0,
∴V(x)在(0,
]单调递增,
∴Vmax=V(
)=
总之,0<c<
时,则当x=时
,Vmax=V(
)=
;
若 c≥
,Vmax=
.
| 1 |
| 2 |
铁皮箱的高度x与底面正方形的边长1-2x的比值
| x |
| 1-2x |
| c |
| 1+2c |
由均值不等式知V=2(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 27 |
当
| 1 |
| 2 |
| 1 |
| 6 |
①当
| 1 |
| 6 |
| c |
| 1+2c |
| 1 |
| 4 |
| 2 |
| 27 |
②当
| 1 |
| 6 |
| c |
| 1+2c |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
则V′(x)在(0,
| 1 |
| 6 |
∴V'(x)≥V'(
| c |
| 1+2c |
| 1 |
| 6 |
∴V(x)在(0,
| c |
| 1+2c |
∴Vmax=V(
| c |
| 1+2c |
| c |
| (1+2c)3 |
总之,0<c<
| 1 |
| 4 |
| c |
| 1+2c |
| c |
| 1+2c |
| c |
| (1+2c)3 |
若 c≥
| 1 |
| 4 |
| 2 |
| 27 |

练习册系列答案
相关题目
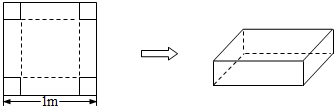 如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值. 某村计划建造一个室内面积为800m2的矩形蔬菜温室(如图).在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.设矩形温室的左侧边长为am,后侧边长为bm,蔬菜的种植面积为Sm2.
某村计划建造一个室内面积为800m2的矩形蔬菜温室(如图).在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.设矩形温室的左侧边长为am,后侧边长为bm,蔬菜的种植面积为Sm2.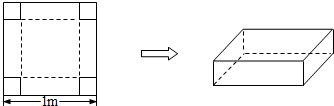 如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.