题目内容
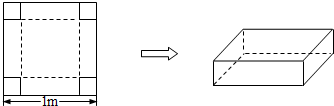
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.
【答案】分析:先求出长方体的底面正方形的边长和高,便可求出长方体的容积V解析式,把容积V变形后使用基本不等式求出最大值,注意分析等号成立条件能否满足,当等号成立条件不能满足时,利用导数值的符号确定函数的单调性,由单调性确定函数的最大值.
解答:解:长方体的底面正方形的边长为1-2x,高为x,所以,容积V=4(x- )2x,
)2x,
铁皮箱的高度x与底面正方形的边长1-2x的比值 ≤c,得 0<x≤
≤c,得 0<x≤ ,
,
由均值不等式知V=2( -x)(
-x)( -x)(2x)≥
-x)(2x)≥ ,
,
当 -x=2x,即x=
-x=2x,即x= 时等号成立.
时等号成立.
①当 ≤
≤ ,即 c≥
,即 c≥ ,Vmax=
,Vmax= ;
;
②当 ≤
≤ ,即 0<c<
,即 0<c< 时,V'(x)=12(x-
时,V'(x)=12(x- ) 2-
) 2- ,
,
则V′(x)在(0, )上单调递减,
)上单调递减,
∴V'(x)≥V'( )>V'(
)>V'( )=0,
)=0,
∴V(x)在(0, ]单调递增,
]单调递增,
∴Vmax=V( )=
)=
总之,0<c< 时,则当x=时
时,则当x=时 ,Vmax=V(
,Vmax=V( )=
)= ;
;
若 c≥ ,Vmax=
,Vmax= .
.
点评:此题是一道应用题,主要还是考查导数的定义及利用导数来求区间函数的最值,利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力,解题的关键是求导要精确.
解答:解:长方体的底面正方形的边长为1-2x,高为x,所以,容积V=4(x-
 )2x,
)2x,铁皮箱的高度x与底面正方形的边长1-2x的比值
 ≤c,得 0<x≤
≤c,得 0<x≤ ,
,由均值不等式知V=2(
 -x)(
-x)( -x)(2x)≥
-x)(2x)≥ ,
,当
 -x=2x,即x=
-x=2x,即x= 时等号成立.
时等号成立.①当
 ≤
≤ ,即 c≥
,即 c≥ ,Vmax=
,Vmax= ;
;②当
 ≤
≤ ,即 0<c<
,即 0<c< 时,V'(x)=12(x-
时,V'(x)=12(x- ) 2-
) 2- ,
,则V′(x)在(0,
 )上单调递减,
)上单调递减,∴V'(x)≥V'(
 )>V'(
)>V'( )=0,
)=0,∴V(x)在(0,
 ]单调递增,
]单调递增,∴Vmax=V(
 )=
)=
总之,0<c<
 时,则当x=时
时,则当x=时 ,Vmax=V(
,Vmax=V( )=
)= ;
;若 c≥
 ,Vmax=
,Vmax= .
.点评:此题是一道应用题,主要还是考查导数的定义及利用导数来求区间函数的最值,利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力,解题的关键是求导要精确.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
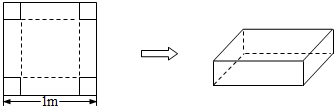 如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值. 某村计划建造一个室内面积为800m2的矩形蔬菜温室(如图).在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.设矩形温室的左侧边长为am,后侧边长为bm,蔬菜的种植面积为Sm2.
某村计划建造一个室内面积为800m2的矩形蔬菜温室(如图).在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.设矩形温室的左侧边长为am,后侧边长为bm,蔬菜的种植面积为Sm2.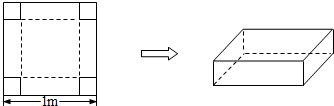 如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.
如图,在边长为1m的正方形铁皮的四角切去边长为x的小正方形,再把它的边沿虚线折起,做成一个无盖的方底铁皮箱,容积为V,并规定:铁皮箱的高度x与底面正方形的边长的比值不超过正常数c,求V的最大值,并写出相应的x的值.