Question

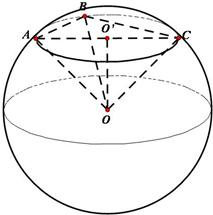A、B、C是球面上三点，已知弦（连接球面上两点的线段）AB=18cm，BC=24cm，AC=30cm，平面ABC与球心的距离恰好为球半径的一半，求球的表面积和体积．

Answer 1

分析：根据题意得三角形ABC是直角三角形，AC是斜边，中点为O′，OA=OB=OC是半径，求出OO′，利用平面ABC与球心的距离恰好为球半径的一半，求出半径，即可求出球O的表面积和体积．

解答：解：球面上三点A、B、C，平面ABC与球面交于一个圆，三点A、B、C在这个圆上
∵AB=18，BC=24，AC=30，
∴AC²=AB²+BC²，∴AC为这个圆的直径，AC中点O′圆心
球心O到平面ABC的距离即OO′=球半径的一半=

1

2

R
△OO′A中，∠OO′A=90°，OO′=

1

2

R，AO′=

1

2

AC=30×

1

2

=15，OA=R
由勾股定理（

1

2

R）²+15²=R²，

3

4

R²=225
解得R=10

3

．
球的表面积S=4πR²=1200π（cm²）；
和体积V=

4

3

πR3=

4

3

×π× (10

3

)3=4000

3

π（cm³）．

点评：本题考查球的体积和表面积、空间想象能力，计算能力，确定三角形ABC的形状以及利用平面ABC与球心的距离恰好为球半径的一半，是解好本题是前提．是基础题，