题目内容
设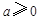 ,
,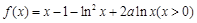 .
.
(1)令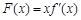 ,讨论
,讨论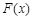 在
在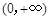 内的单调性并求极值;
内的单调性并求极值;
(2)求证:当 时,恒有
时,恒有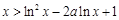 .
.
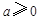 ,
,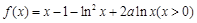 .
.(1)令
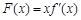 ,讨论
,讨论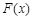 在
在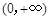 内的单调性并求极值;
内的单调性并求极值;(2)求证:当
 时,恒有
时,恒有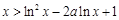 .
.(1) 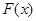 在
在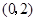 内是减函数,在
内是减函数,在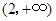 内是增函数, 在
内是增函数, 在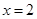 处取得极小值
处取得极小值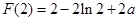 ;(2)详见解析.
;(2)详见解析.
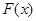 在
在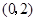 内是减函数,在
内是减函数,在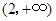 内是增函数, 在
内是增函数, 在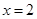 处取得极小值
处取得极小值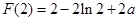 ;(2)详见解析.
;(2)详见解析.试题分析:(1)先根据求导法求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间及极值即可.
(2)欲证x>ln2x-2a ln x+1,即证x-1-ln2x+2alnx>0,也就是要证f(x)>f(1),根据第一问的单调性即可证得.
试题解析:解(1)解:根据求导法则有
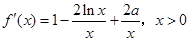 ,
,故
 , 3分
, 3分于是
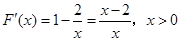 ,
,列表如下:
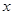 | 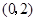 | 2 | 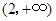 |
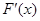 | 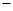 | 0 | 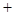 |
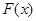 | 递减 | 极小值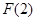 | 递增 |
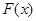 在
在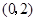 内是减函数,在
内是减函数,在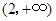 内是增函数,所以,在
内是增函数,所以,在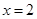 处取得极小值
处取得极小值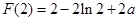 . 6
. 6(2)证明:由
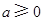 知,
知,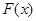 的极小值
的极小值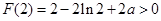 .
.于是由上表知,对一切
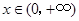 ,恒有
,恒有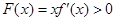 .
.从而当
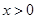 时,恒有
时,恒有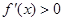 ,故
,故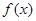 在
在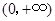 内单调增加.
内单调增加.所以当
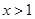 时,
时, ,即
,即 .
.故当
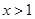 时,恒有
时,恒有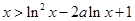 . .12
. .12
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
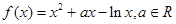 .
.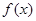 的单调区间;
的单调区间;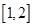 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围;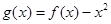 ,是否存在实数a,当
,是否存在实数a,当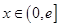 (e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.
(e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.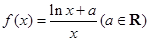 .
.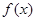 的单调区间和极值;
的单调区间和极值;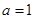 ,且
,且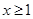 时,证明:
时,证明: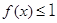 .
. ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.
 -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.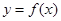 的导函数
的导函数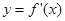 的图象,给出下列命题:
的图象,给出下列命题: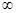 ,-2)上单调递减
,-2)上单调递减
 在区间[-1,2]上是减函数,那么b+c( )
在区间[-1,2]上是减函数,那么b+c( )
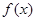 是定义在
是定义在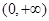 上的非负可导函数,且满足
上的非负可导函数,且满足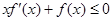 ,对任意正数
,对任意正数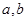 ,若
,若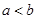 ,则必有( )
,则必有( )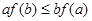
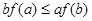
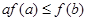
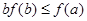
 在定义域内可导,
在定义域内可导,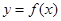 的图像如右图,则导函数
的图像如右图,则导函数 的图像可能是( )
的图像可能是( )
