题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{3}-12x，x＞t}\\{（a-1）x+2，x≤t}\end{array}\right.$，如果对一切实数t，函数f（x）在R上不单调，则实数a的取值范围是a≤1．分析 通过讨论t的范围，确定函数在区间上的单调性，从而求出a的范围即可．
解答 解：x＞t时：f（x）=x3-12x，f′（x）=3x2-12=3（x+2）（x-2），
t＜-2时，f（x）在（t，-2）递增，在（-2，2）递减，在（2，+∞）递增，f（x）不单调，
-2≤t≤2时，f（x）在（t，2）递减，在（2，+∞）递增，f（x）不单调，
t＞2时，f（x）在（t，+∞）单调递增，
如果对一切实数t，函数f（x）在R上不单调，
只需f（x）=（a-1）x+2在（-∞，t]递减，
即a-1＜0，解得：a＜1，显然a=1时，符合题意，
故答案为：a≤1．
点评 本题考查了函数的单调性问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
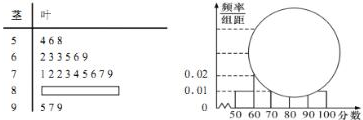某校高一某班的一次数学测试成绩（满分为100分）的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，据此解答如下问题；
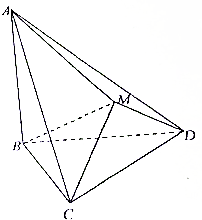如图，△BCD与△MCD都是正三角形，平面MCD⊥平面BCD，AB⊥平面BCD．