Question

（本小题有两个小题供选做，考生只能在①、②题中选做一题！多做不给分）
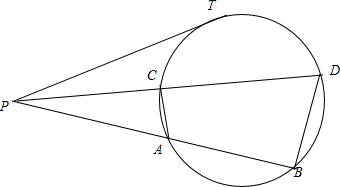
①PT切⊙O于点T，PAB、PCD是割线，AB=35cm，CD=50cm，AC：DB=1：2，则PT=

60 cm

②已知A（ρ₁，θ₁），B（ρ₂，θ₂）则AB=

ρ 2 1 + ρ 2 2 -2ρ1ρ2cos(θ1-θ2)

．

．

Answer 1

分析：①设PA=x，可证明△PAC∽△PDB，则

AC

BD

=

PA

PD

，由已知得，PD=2PA，则由切割线定理得PA•PB=PC•PD，即x（x+35）=2x（2x-35），求解即可．
②在△AOB中，OA=ρ₁，OB=ρ₂，∠AOB=|θ₁-θ₂|+2kπ，k∈z． 由余弦定理可求得 AB 的值．

解答：解：①设PA=x，∵∠PAC=∠D，∴△PAC∽△PDB，∴

AC

BD

=

PA

PD

． 
∵AC：DB=1：2，∴PD=2PA，∴由切割线定理得，PA•PB=PC•PD，即x（x+35）=2x（2x-35），解得x=45．
再由切割线定理可得 PT=

PA•PB

=

45×(45+35)

=60，
故答案为：60．

②已知A（ρ₁，θ₁），B（ρ₂，θ₂ ），在△AOB中，OA=ρ₁，OB=ρ₂，∠AOB=|θ₁-θ₂|+2kπ，k∈z． 由余弦定理可得
AB=

OA2+OB2-2OA•OBcos∠AOB

=

ρ 2 1 + ρ 2 2 -2ρ1ρ2cos[2kπ+(θ1-θ2)]

=

ρ 2 1 + ρ 2 2 -2ρ1ρ2cos(θ1-θ2)

．
故答案为：

ρ 2 1 + ρ 2 2 -2ρ1ρ2cos(θ1-θ2)

．

点评：本题考查了切割线定理和相似三角形的判定和性质，余弦定理的应用，属于基础题．