题目内容
【题目】设函数![]() 的单调减区间是
的单调减区间是![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)若对任意的![]() ,关于
,关于![]() 的不等式
的不等式![]() 在
在
![]() 时有解,求实数
时有解,求实数![]() 的取值范围。
的取值范围。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)f'(x)=3ax2+2bx+c.由f(x)的单调减区间是(1,2),知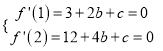 ,由此能求出f(x)的解析式.
,由此能求出f(x)的解析式.
(2)由(1)得f'(x)=3x2﹣9x+6=3(x﹣1)(x﹣2),当x∈[2,+∞)时,f'(x)≥0,故f(x)在[2,+∞)单调递增,所以f(x)min=f(2)=3.要使关于x的不等式![]() 在x∈[2,+∞)时有解,只需
在x∈[2,+∞)时有解,只需![]() 在m∈(0,2]恒成立.由此能求出实数t的取值范围.
在m∈(0,2]恒成立.由此能求出实数t的取值范围.
试题解析:
⑴![]() .
.
∵![]() 的单调减区间是(1,2),∴
的单调减区间是(1,2),∴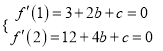 ,
,
∴![]() ∴
∴![]() .
.
⑵由⑴得![]() ,
,
当![]() 时,
时, ![]() ≥0,∴
≥0,∴![]() 在
在![]() 单调递增,∴
单调递增,∴![]()
![]() .
.
要使关于![]() 的不等式
的不等式![]() 在
在![]() 时有解,
时有解,
即![]() ,即
,即![]() 对任意
对任意![]() 恒成立,
恒成立,
只需![]() 在
在![]() 恒成立.
恒成立.
设![]() ,
, ![]() ,则
,则![]() 。
。![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() .
.![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目