题目内容
12.在△ABC中,三角A,B,C满足关系式:sin2A+sin2B=sin2C+sinAsinB,G是△ABC垂心,且满足$\overrightarrow{CG}$•$\overrightarrow{CA}$=6,则△ABC的面积S△ABC=( )| A. | 3 | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 通过正弦定理与余弦定理求出C的余弦函数值,结合向量的数量积,即可求解三角形的面积.
解答 解:由正弦定理化简sin2A+sin2B=sin2C+sinAsinB,得:a2+b2=c2+ab,即a2+b2-c2=ab,
∴cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∵B为三角形内角,∴C=$\frac{π}{3}$,
G是△ABC垂心,且满足$\overrightarrow{CG}$•$\overrightarrow{CA}$=$\left|\overrightarrow{CG}\right|\left|\overrightarrow{CA}\right|$cos∠ACG=6,
∵$\left|\overrightarrow{CG}\right|\left|\overrightarrow{CA}\right|$×cos∠ACG=$\left|\overrightarrow{AC}\right|\left|\overrightarrow{BC}\right|cosC$=6,
∴$\left|\overrightarrow{AC}\right|\left|\overrightarrow{BC}\right|=12$,
则△ABC的面积S△ABC=$\frac{1}{2}$×$\left|\overrightarrow{AC}\right|\left|\overrightarrow{BC}\right|sinC=\frac{1}{2}×12×\frac{\sqrt{3}}{2}$=$3\sqrt{3}$.
故选:C.
点评 此题考查了正弦定理、余弦定理,三角形面积公式,以及平面向量的数量积运算,熟练掌握定理及公式是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | {x|-3<x≤4} | B. | {x|3<x<4} | C. | {x|3<x≤4} | D. | {x|-3<x<3} |

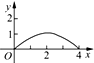
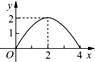
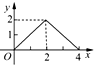
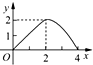
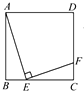 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )