题目内容
已知O为△ABC的外心, , 若
, 若 ,且32x+25y=25,则
,且32x+25y=25,则 == .
== .
10
解析试题分析:解:如图.
若 ,则
,则 ,
,
O为外心,D,E为中点,OD,OE分别为两中垂线. =|
=| |(|
|(| |cos∠DAO)=|
|cos∠DAO)=| |×AD=|
|×AD=| |×
|× ×|
×| |=16×8=128
|=16×8=128
同样地, =
= |
| |2=100
|2=100
所以 128x+100y=4(32x+25y)=100
128x+100y=4(32x+25y)=100
∴| |=10
|=10
故答案为:10.
考点:三角形五心;向量的模;平面向量的基本定理及其意义
点评:本题考查三角形外心的性质,向量数量积的运算、向量模的求解.本题中进行了合理的转化 ,并根据外心的性质化简求解
,并根据外心的性质化简求解

练习册系列答案
相关题目
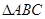 中,
中, 、
、 分别为边
分别为边 、
、 的中点.
的中点.  为边
为边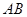 上的点,且
上的点,且 ,若
,若 ,
, ,则
,则 的值为 .
的值为 .
 中,已知
中,已知 ,
, 为
为 的中点,若
的中点,若 为正方形 内(含边界)任意一点,则
为正方形 内(含边界)任意一点,则 的取值范围是 .
的取值范围是 . 
 等于 。
等于 。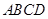 中,
中, ,
, ,
,  ,
, ,点
,点 是梯形
是梯形 是
是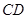 边的中点,则
边的中点,则 的最大值是____.
的最大值是____.
 =(2,1),
=(2,1), =(-3,-4),则向量
=(-3,-4),则向量 满足
满足 (
( ),且
),且 是
是 的等差中项,则数列
的等差中项,则数列 是单位向量,若向量
是单位向量,若向量 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .