题目内容
对?a、b∈R，运算“⊕”、“?”定义为a⊕b=
，a?b=
，则下列各式恒成立的是（ ）
①a?b+a⊕b=a+b；
②a?b-a⊕b=a-b；
③[a?b]•[a⊕b]=a•b
④[a?b]÷[a⊕b]=a÷b．
|
|
①a?b+a⊕b=a+b；
②a?b-a⊕b=a-b；
③[a?b]•[a⊕b]=a•b
④[a?b]÷[a⊕b]=a÷b．
| A、①④ | B、②③ | C、①③ | D、②④ |
分析：根据a⊕b=
，可知“⊕”取其“小”；a?b=
，可知“?”取其“大”；对四个选项分a≥b与a＜b逐项分析即可得到答案．
|
|
解答：解：∵a⊕b=
，a?b=
，
∴当a≥b时，a?b=a，a⊕b=b，①②③④都对；
当a＜b时a?b=b，a⊕b=a，①③正确，②④错误；
故选C．
|
|
∴当a≥b时，a?b=a，a⊕b=b，①②③④都对；
当a＜b时a?b=b，a⊕b=a，①③正确，②④错误；
故选C．
点评：本题考查函数恒成立问题，关键是对“⊕”取其“小”“?”取其“大”的理解，属于容易题．
练习册系列答案
相关题目
对?a、b∈R，运算“?”、“?”定义为：a?b=
，a?b=
，则下列各式其中不恒成立的是（ ）
（1）a?b+a?b=a+b （2）a?b-a?b=a-b （3）[a?b]?[a?b]=a?b （4）[a?b]÷[a?b]=a÷b．
|
|
（1）a?b+a?b=a+b （2）a?b-a?b=a-b （3）[a?b]?[a?b]=a?b （4）[a?b]÷[a?b]=a÷b．
| A、（1）、（3） |
| B、（2）、（4） |
| C、（1）、（2）、（3） |
| D、（1）、（2）、（3）、（4） |
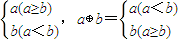，则下列各式中恒成立的是（ ）
，则下列各式中恒成立的是（ ）