题目内容
对?a，b∈R，运算“?”、“⊕”定义为：a?b=
，a⊕b=
，则下列各式中恒成立的是（ ）
①（sinx?cosx）+（sinx⊕cosx）=sinx+cosx，
②（2x?x2）-（2x⊕x2）=2x-x2，
③（sinx?cosx）•（sinx⊕cosx）=sinx•cosx，
④（2x⊕x2）-（2x?x2）=2x-x2．
|
|
①（sinx?cosx）+（sinx⊕cosx）=sinx+cosx，
②（2x?x2）-（2x⊕x2）=2x-x2，
③（sinx?cosx）•（sinx⊕cosx）=sinx•cosx，
④（2x⊕x2）-（2x?x2）=2x-x2．
| A、①②③④ | B、①②③ |
| C、①③ | D、②④ |
分析：结合新定义，验算①②③④，即可判断正确选项．
解答：解：由题意可知：①（sinx?cosx）+（sinx⊕cosx）=sinx+cosx．③（sinx?cosx）•（sinx⊕cosx）=sinx•cosx，加法与乘法满足交换律，正确；
②（2x?x2）-（2x⊕x2）=2x-x2，④（2x⊕x2）-（2x?x2）=2x-x2不恒成立，
故选C．
②（2x?x2）-（2x⊕x2）=2x-x2，④（2x⊕x2）-（2x?x2）=2x-x2不恒成立，
故选C．
点评：本题是基础题，考查新定义的应用，考查发现问题解决问题的能力，常考题型．
练习册系列答案
轻松暑假总复习系列答案
相关题目
对?a、b∈R，运算“⊕”、“?”定义为a⊕b=
，a?b=
，则下列各式恒成立的是（ ）
①a?b+a⊕b=a+b；
②a?b-a⊕b=a-b；
③[a?b]•[a⊕b]=a•b
④[a?b]÷[a⊕b]=a÷b．
|
|
①a?b+a⊕b=a+b；
②a?b-a⊕b=a-b；
③[a?b]•[a⊕b]=a•b
④[a?b]÷[a⊕b]=a÷b．
| A、①④ | B、②③ | C、①③ | D、②④ |
对?a、b∈R，运算“?”、“?”定义为：a?b=
，a?b=
，则下列各式其中不恒成立的是（ ）
（1）a?b+a?b=a+b （2）a?b-a?b=a-b （3）[a?b]?[a?b]=a?b （4）[a?b]÷[a?b]=a÷b．
|
|
（1）a?b+a?b=a+b （2）a?b-a?b=a-b （3）[a?b]?[a?b]=a?b （4）[a?b]÷[a?b]=a÷b．
| A、（1）、（3） |
| B、（2）、（4） |
| C、（1）、（2）、（3） |
| D、（1）、（2）、（3）、（4） |
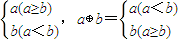，则下列各式中恒成立的是（ ）
，则下列各式中恒成立的是（ ）