题目内容
已知 =(sinθ,-2)与
=(sinθ,-2)与 =(1,cosθ)互相垂直,其中θ∈(0,
=(1,cosθ)互相垂直,其中θ∈(0, ).
).
(1)求sinθ和cosθ的值;
(2)若sin(θ-j)= ,0<j<
,0<j< ,求j的值.
,求j的值.
解:(1)因为 与
与 互相垂直,
互相垂直,
所以 •
• =0.
=0.
所以sinθ-2cosθ=0,即sinθ=2cosθ.
因为sin2θ+cos2θ=1,
所以(2cosθ)2+cos2θ=1.
解得cos2θ= .则sin2θ=
.则sin2θ= .
.
因为θ∈(0, ),
),
所以sinθ>0,cosθ>0,
所以sinθ= ,cosθ=
,cosθ= .
.
(2)因为0<j< ,0<θ<
,0<θ< ,所以-
,所以- <θ-j<
<θ-j< ,
,
所以cos(θ-j)=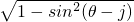 =
= ,
,
所以cosj=cos[θ-(θ-j)]=cosθcos(θ-j)+sinθsin(θ-j)= .所以j=
.所以j= .
.
分析:(1)先根据 与
与 互相垂直得到
互相垂直得到 •
• =0,然后将
=0,然后将 =(sinθ,-2)与
=(sinθ,-2)与 =(1,cosθ)代入可得到sinθ=2cosθ,再由同角三角函数的基本关系和θ的取值范围可求得sinθ和cosθ的值.
=(1,cosθ)代入可得到sinθ=2cosθ,再由同角三角函数的基本关系和θ的取值范围可求得sinθ和cosθ的值.
(2)先根据j与θ的范围确定θ-j的范围,进而根据同角三角函数的基本关系可求得cos(θ-j)的值,再由cosj=cos[θ-(θ-j)]和两角和与差的余弦公式可求得最后答案.
点评:本题主要考查向量垂直与数量积的关系、同角三角函数的基本关系和两角和与差的公式.考查基础知识的综合应用,三角函数与向量的综合题是高考的热点问题,每年必考,一定要加强练习.
 与
与 互相垂直,
互相垂直,所以
 •
• =0.
=0.所以sinθ-2cosθ=0,即sinθ=2cosθ.
因为sin2θ+cos2θ=1,
所以(2cosθ)2+cos2θ=1.
解得cos2θ=
 .则sin2θ=
.则sin2θ= .
.因为θ∈(0,
 ),
),所以sinθ>0,cosθ>0,
所以sinθ=
 ,cosθ=
,cosθ= .
.(2)因为0<j<
 ,0<θ<
,0<θ< ,所以-
,所以- <θ-j<
<θ-j< ,
,所以cos(θ-j)=
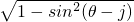 =
= ,
,所以cosj=cos[θ-(θ-j)]=cosθcos(θ-j)+sinθsin(θ-j)=
 .所以j=
.所以j= .
.分析:(1)先根据
 与
与 互相垂直得到
互相垂直得到 •
• =0,然后将
=0,然后将 =(sinθ,-2)与
=(sinθ,-2)与 =(1,cosθ)代入可得到sinθ=2cosθ,再由同角三角函数的基本关系和θ的取值范围可求得sinθ和cosθ的值.
=(1,cosθ)代入可得到sinθ=2cosθ,再由同角三角函数的基本关系和θ的取值范围可求得sinθ和cosθ的值.(2)先根据j与θ的范围确定θ-j的范围,进而根据同角三角函数的基本关系可求得cos(θ-j)的值,再由cosj=cos[θ-(θ-j)]和两角和与差的余弦公式可求得最后答案.
点评:本题主要考查向量垂直与数量积的关系、同角三角函数的基本关系和两角和与差的公式.考查基础知识的综合应用,三角函数与向量的综合题是高考的热点问题,每年必考,一定要加强练习.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目