题目内容
设f(x)=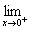 当a、b为何值时,函数f(x)在定义区间内连续?
当a、b为何值时,函数f(x)在定义区间内连续?
解:∵![]() f(x)=
f(x)=![]() (x2+1)=1,
(x2+1)=1,![]() f(x)=
f(x)=![]() (x+a)=a=f(0),
(x+a)=a=f(0),
∴当a=1时,
![]() f(x)=
f(x)=![]() f(x)=f(0),即f(x)在x=0处连续.
f(x)=f(0),即f(x)在x=0处连续.
∵![]() f(x)
f(x)
=![]() (x2+1)=2=f(1).
(x2+1)=2=f(1).
![]() f(x)=
f(x)=![]()
![]() =b,
=b,
∴当b=2时,
![]() f(x)=
f(x)=![]() f(x)=f(1).即f(x)在x=1处连续.
f(x)=f(1).即f(x)在x=1处连续.
综上,当a=1,b=2时,函数f(x)在定义区间内连续.

练习册系列答案
相关题目
题目内容
设f(x)=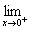 当a、b为何值时,函数f(x)在定义区间内连续?
当a、b为何值时,函数f(x)在定义区间内连续?
解:∵![]() f(x)=
f(x)=![]() (x2+1)=1,
(x2+1)=1,![]() f(x)=
f(x)=![]() (x+a)=a=f(0),
(x+a)=a=f(0),
∴当a=1时,
![]() f(x)=
f(x)=![]() f(x)=f(0),即f(x)在x=0处连续.
f(x)=f(0),即f(x)在x=0处连续.
∵![]() f(x)
f(x)
=![]() (x2+1)=2=f(1).
(x2+1)=2=f(1).
![]() f(x)=
f(x)=![]()
![]() =b,
=b,
∴当b=2时,
![]() f(x)=
f(x)=![]() f(x)=f(1).即f(x)在x=1处连续.
f(x)=f(1).即f(x)在x=1处连续.
综上,当a=1,b=2时,函数f(x)在定义区间内连续.
