题目内容
如图1-5,梯形ABCD中,BA∥CD,对角线AC、BD交于点E,过E作FG∥AB,交AD、BC于G、F点.(1)求证:EF=EG.
(2)求证:
+
=
.
(3)若直线l平行于底边但不过E,与BC、AC、BD、AD分别交于F′、M、N、G′,试问:F′M与G′N有何关?并说明理由.
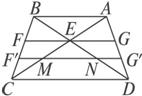
图1-5
证明:(1)∵AB∥FG∥CD,
∴
===.
∴EF=EG.
(2)∵EF∥AB
=
AB=
.
同理,CD=
.
由(1)知EF=EG.
∴
+
=
.
(3)∵FG∥F′G′,
∴
.
而EF=GE.
∴F′M=G′N.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
（2013•泉州模拟）如图，等腰梯形ABCD中，AB∥CD且AB=2，AD=1，DC=2x（x∈（0，1））．以A，B为焦点，且过点D的双曲线的离心率为e1；以C，D为焦点，且过点A的椭圆的离心率为e2，则e1+e2的取值范围为 （ ）
