题目内容
如图求证:OD2=AD·BC.
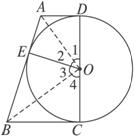
图
证明:连结OA、OB.
∵OD⊥AD,OE⊥AE,
∴在Rt△OAE、Rt△OAD中,![]()
∴△OAE≌△OAD.∴AD=AE,∠1=∠2.
同理,BC=BE,∠3=∠4.∴∠2+∠3=∠1+∠4=90°.
在Rt△AOB中,∵OE⊥AB,
∴OE2=AE·BE.∴OD2=AD·BC.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
如图求证:OD2=AD·BC.

图
证明:连结OA、OB.
∵OD⊥AD,OE⊥AE,
∴在Rt△OAE、Rt△OAD中,![]()
∴△OAE≌△OAD.∴AD=AE,∠1=∠2.
同理,BC=BE,∠3=∠4.∴∠2+∠3=∠1+∠4=90°.
在Rt△AOB中,∵OE⊥AB,
∴OE2=AE·BE.∴OD2=AD·BC.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案