题目内容
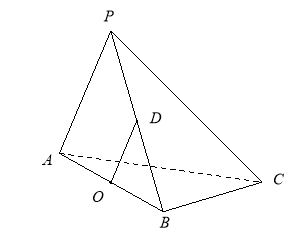
【题目】四棱锥
中，底面
是
的菱形，侧面
为正三角形，其所在平面垂直于底面.
（1）若
为线段
的中点，求证：
平面
；
（2）若
为边
的中点，能否在棱
上找到一点
，使平面
平面？并证明你的结论.
【答案】（见解析；（2）见解析．
【解析】分析：（1）取
的中点，利用等腰三角形的“三线合一”得到线线垂直，进而利用线面垂直的判定定理进行证明；（2）先利用面面垂直的性质得到线面垂直，进而得到面面垂直，再利用面面垂直的性质得到线线垂直，利用平行四边形确定点的位置．
详解：（1）如图，取中点
，连接
，
，
，
∵ 
为等边三角形，∴ 
，
在
中，
，
，
∴ 为等边三角形，∴ 
，
∴ 
平面
.
（2）连接
与
相交于点
，
在
中，作
，交
于点
，
∵ 平面
平面
，∴ 
平面，
∴ 
平面，
∴ 平面
平面，
易知四边形
为平行四边形，
∴ 是的中点，∴ 是的中点，
∴ 在上存在一点，即为的中点，使得平面
平面.
练习册系列答案
相关题目
【题目】辽宁号航母纪念章从2012年10月5日起开始上市，通过市场调查，得到该纪念章每
枚的市场价
（单位：元）与上市时间
（单位：天）的数据如下：
上市时间 |
|
|
|
市场价 |
|
|
|
（1）根据上表数据，从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价与上市时间的变化关系：①
；②
；③
；
（2）利用你选取的函数，求辽宁号航母纪念章市场价最低时的上市天数及最低的价格；
（3）设你选取的函数为
，若对任意实数
，关于的方程
恒有个想异实数根，求
的取值范围.
