题目内容
设0<a<1,x和y满足logax+3logxa-logxy=3,如果y有最大值
| ||
| 4 |
分析:把原方程转化为logax+
-
=3,即logay=loga2x-3logax+3=(logax-
)2+
,然后利用二次函数的性质求如果y有最大值
时a和x的值.
| 3 |
| logax |
| logay |
| logax |
| 3 |
| 2 |
| 3 |
| 4 |
| ||
| 4 |
解答:解:原式可化为logax+
-
=3,即logay=loga2x-3logax+3=(logax-
)2+
,知当logax=
时,logay有最小值
.
∵0<a<1,∴此时y有最大值a
.
根据题意a
=
?a=
.这时x=a
=(
)
=
.
| 3 |
| logax |
| logay |
| logax |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
∵0<a<1,∴此时y有最大值a
| 3 |
| 4 |
根据题意a
| 3 |
| 4 |
| ||
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 8 |
点评:本题是已知函数的最值,求函数式中的字母参数的值.这类问题,也是常见题型之一.

练习册系列答案
相关题目
 ,求这时a和x的值.
,求这时a和x的值.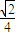 ,求这时a和x的值.
,求这时a和x的值.